Bogen in projectieve vlakken
Kenneth Genbrugge
Studentennummer: 01004174
Promotor: Prof. dr. Leo Storme
Co-promotor: Maarten De Boeck
Universiteit GentFaculteit Wetenschappen
Vakgroep Wiskunde: Analyse, Logica en Discrete Wiskunde
Masterproef ingediend tot het behalen van de academische graad van master in de wiskunde, afstudeerrichting zuivere wiskunde.
Bogen in projectieve vlakken
Kenneth Genbrugge
Studentennummer: 01004174
Promotor: Prof. dr. Leo Storme
Co-promotor: Maarten De Boeck
Universiteit GentFaculteit Wetenschappen
Vakgroep Wiskunde: Analyse, Logica en Discrete Wiskunde
Masterproef ingediend tot het behalen van de academische graad van master in de wiskunde, afstudeerrichting zuivere wiskunde.
0
Voorwoord
Without ambition one starts nothing. Without work one finishes nothing. The price will not be sent to you. You have to win it.
Ralph Waldo Emerson (1803 1822)
Voor u ligt de thesis Bogen in projectieve vlakken. Deze is geschreven in het kader van mijn afstud eren aan de opleiding Master in de wiskunde, afstudeerrichting zuivere wiskunde. Met deze schriftelijke uiteenzetting breng ik een einde aan een boeiend leerproces dat zich uitstrekte over meerdere jaren en over meerdere facetten.
Uit persoonlijke ervaringen kan ik concluderen dat dit leerproces niet zonder obstakels was. Ik startte mijn universitaire loopbaan met een ondoordachte keuze, waar ik na enkele weken al spijt van had. Ik besloot om een sprong in het duister te wagen en koos voor een opleiding voor leerkracht Latijn en wiskunde. Uit de lessen, vele practica en de stages werd mij duidelijk dat ik een goede keuze had gemaakt. Na het behalen van dat diploma, wou ik nog een stap verder zetten. Met de bemoedigende woorden van V. Ver Gucht op zak begon ik aan de opleiding wiskunde aan de UGent.
De omschakeling van een professionele bachelor aan de Arteveldehogeschool naar een academische bachelor aan de UGent, was een veel grotere stap dan ik kon inschatten. De vele tegenslagen deden mij twijfelen aan mijn capaciteiten, maar ik wou niet snel opgeven. Het feit dat ik echter vrijstellingen behaalde voor mijn minor in deze opleiding, gaf me een boost om dit alles tot een goed eind te brengen. Daarnaast kon ik rekenen op een hechte vriendengroep waar men elkaar hielp bij vragen en onduide lijkheden. En indien zij mij niet konden helpen, mocht ik steeds elke professor of assistent contacteren opdat deze mij zouden helpen. Hiervoor mijn oprechte dank.
Na enkele jaren voltijds student te zijn, kwam de mogelijkheid voor mij om ook een stap in het onderwijs te zetten. Het was echter niet evident om mijn professioneel leven te combineren met mijn studies. Zo moest ik mijn tijdsbesteding verdelen over het voorbereiden van lessen, het bijwonen van vergaderingen, het zelf volgen van lessen, het studeren van cursussen en het schrijven van mijn masterproef.
Daarom wil ik van deze opportuniteit gebruik maken om volgende mensen te bedanken. Zonder hun hulp zou dit niet gelukt zijn. Allereerst wil ik professor L. Storme bedanken om mij dit onderwerp aan te bieden. De tweede persoon die mij enorm geholpen heeft tijdens het schrijven van mijn thesis, is Maarten De Boeck. Vanaf het begin heeft hij mij met veel raad, advies, hulp en geduld doorheen dit werk begeleid. Hiervoor mijn oprechte dank.
Graag wil ik ook mijn dank uitdrukken tegenover mijn collega’s en directie. In de eerste plaats bedank ik M. Versprille, die het mogelijk maakte om het leraar zijn en mijn studies te combineren. Zij stond open om mij zoveel mogelijk kansen te bieden om mijn studies tot een goed einde te brengen. Ondanks de moeilijke combinatie, bleef zij vertrouwen hebben. Ook bedank ik mijn collega’s, in het bijzonder de collega’s wiskunde, voor de blijvende steun, het advies, de tips en het luisterend oor. Het is een plezier om deel te mogen uitmaken van deze warme school.
Daarnaast bedank ik mijn ouders voor het blinde vertrouwen in mijn kunnen. Ze boden mij vele kansen aan en waren een blijvende steun en toeverlaat. En tenslotte wil ik mijn vriendin, Hendrickje, bedanken voor de continue steun, het vele begrip, de grote interesse en de vele liefde gedurende dit schrijfproces. Daarnaast nam ze ook de tijd om de hele tekst te na te lezen. Ze stond me ook bij tijdens het schrijven van de Engelstalige samenvatting. Zonder haar hulp had ik dit eindproduct niet kunnen voorleggen.
Kenneth Genbrugge,
0
Toelating tot bruikleen
“De auteur geeft de toelating deze masterproef voor consultatie beschikbaar te stellen en delen van de masterproef te kopiëren voor persoonlijk gebruik. Elk ander gebruik valt onder de beperkingen van het auteursrecht, in het bijzonder met betrekking tot de verplichting de bron uitdrukkelijk te vermelden bij het aanhalen van resultaten uit deze masterproef.”
“The author gives permission to make this master dissertation available for consultation and to copy parts of this master dissertation for personal use. In the case of any other use, the limitations of the copyright have to be respected, in particular with regard to the obligation to state expressly the source when quoting results from this master dissertation.”
Kenneth Genbrugge,
0
Inhoudsopgave
1 Inleidende begrippen 1 1.1 Eindige velden . . . 2 1.1.1 Definities, notaties . . . 2 1.1.2 Morfismen . . . 3 1.1.3 Spoor . . . 6 1.1.4 Functies . . . 7 1.1.5 Vergelijkingen en wortels . . . 8 1.2 Projectieve ruimten . . . 10 1.2.1 Definities . . . 101.2.2 Karakterisering van deelruimten . . . 12
1.2.3 Polariteiten en perspectiviteiten . . . 13
1.2.4 Kegelsneden . . . 15
1.2.5 Hermitische krommen . . . 17
1.2.6 Het affien vlak AG(2,q) . . . 17
1.3 Getaltheorie . . . 19
1.3.1 Grootste gemeenschappelijke deler . . . 19
1.3.2 Lineaire congruenties . . . 19
1.3.3 Stelling van Lucas . . . 20
2 Kbogen van graad 2 22 2.1 Een kboog van graad 2 . . . 23
Inhoudsopgave
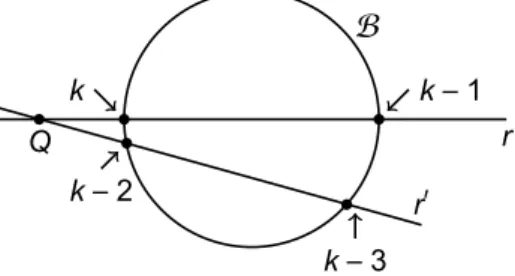
2.2 Tellingen met betrekking tot de bisecanten . . . 25
2.3 Tellingen met betrekking tot de raaklijnen . . . 28
2.4 Tellingen met betrekking tot de externe rechten . . . 33
2.5 Khoeken en kzijden . . . 36
2.6 Ovalen en hyperovalen . . . 40
2.6.1 Bisecanten, raaklijnen en externe rechten . . . 40
2.6.2 Stelling van Segre . . . 42
2.6.3 Hyperovalen . . . 48
2.6.4 Translatiehyperovalen . . . 59
2.6.5 Hyperovalen en flocks . . . 65
2.6.6 Synthese . . . 71
2.7 Complete bogen . . . 73
2.7.1 Voorwaarde voor niet complete bogen . . . 73
2.7.2 Complete bogen verschillend van (hyper)ovalen . . . 75
3 Kbogen van hogere graad 87 3.1 Definities en tellingen . . . 88
3.2 Maximale bogen . . . 91
3.2.1 Triviale en niettriviale maximale bogen . . . 91
3.2.2 Maximale bogen in PG(2,q) met q even: Denniston maximale bogen . . . 95
3.2.3 Maximale bogen in PG(2,q) met q even: Mathon maximale bogen . . . 98
3.2.4 Maximale bogen in PG(2,q) met q oneven . . . 113
3.3 Bogen met twee intersectiegetallen . . . 125
3.3.1 Definitie, tellingen en voorwaarden . . . 125
3.3.2 Hermitische bogen . . . 128
A Summary in English 134
B Berekeningen in Sage voor stelling 2.7.13 143
0
Lijst van figuren
1.1 Het projectief vlak PG(2, 2). . . 11
1.2 Het projectief vlak PG(2, 3). . . 11
1.3 Tekening horende bij lemma 1.2.3. . . 12
1.4 Tekening horende bij lemma 1.2.8. . . 15
2.1 Eerste tekening ter ondersteuning van stelling 2.1.4. . . 23
2.2 Tweede tekening ter ondersteuning van stelling 2.1.4. . . 24
2.3 Tekening ter ondersteuning van stelling 2.2.4, (2.2). . . 26
2.4 Tekening ter ondersteuning van stelling 2.2.4, (2.3). . . 27
2.5 Eerste twee tekeningen ter ondersteuning van lemma 2.5.2, (i). . . 37
2.6 Derde tekening ter ondersteuning van lemma 2.5.2, (i), nl. k= 5. . . 38
2.7 Tekening ter ondersteuning van stelling 2.6.5. . . 41
2.8 Tekening 1 ter ondersteuning van lemma 2.6.11. . . 44
2.9 Tekening 2 ter ondersteuning van lemma 2.6.11. . . 44
2.10 Tekening ter ondersteuning van stelling 2.6.12, stap 2. . . 45
2.11 Tekening ter ondersteuning van stelling 2.6.16. . . 48
2.12 Tekening ter ondersteuning van voorbeeld 2.6.18. . . 49
0
Lijst van tabellen
2.1 De waarden l(k, q) voor 1 ≤ k ≤ 5. . . 36
2.2 De waarden L(k, q) voor 2 ≤ k ≤ 6. . . 36
2.3 Het aantal punten niet op de zijden van een khoek voor 2≤ k ≤ 5. . . 38
2.4 Eerste drie klassen van hyperovalen in PG(2, q), q even. . . 71
2.5 Vierde klasse van hyperovalen in PG(2, q), q even. . . 71
2.6 Overige klassen van hyperovalen in PG(2, q), q even. . . 72
2.7 Constanten ci voor kleine bogen. . . 76
1
Inleidende begrippen
Het doel van dit eerste hoofdstuk is om meerdere concepten en begrippen op te lijsten. We gaan er echter van uit dat de lezer al vertrouwd is met de meeste van deze zaken. Kleine, maar noodzakelijke lemma’s kan men ook in dit hoofdstuk terugvinden. Met het oog op een compleet werk, zullen we deze lemma’s ook voorzien van een bewijs. De inhoud van dit hoofdstuk is grotendeels gebaseerd op het werk van Hirschfeld [16] en De Bruyn [10]. We verwijzen naar hun werken indien de lezer een meer uitvoerige uiteenzettingen wenst.
Er zijn in totaal drie delen: een eerste deel over eindige velden, een tweede deel over projectieve ruimten en het laatste deel over getaltheorie en algebra. Bij eindige velden lijsten we eerst enkele begrippen en symbolen. Vervolgens bewijzen we de nodige lemma’s over de elementen van het veld
F
q, morfismen, de spoorafbeelding, Lagrangeinterpolatie en permutatiepolynomen en over de wortels van een kwadratische vergelijking over
F
q.Het stuk over projective ruimten heeft een analoog begin. Ook hier starten we op met een opsomming van vele definities en begrippen. Hierna sommen we de karakterisering van deelruimten op. Daarna definiëren we polariteiten en perspectiviteiten (na de nodige inleidende begrippen). Omdat in de latere hoofdstukken ook vaak gesproken wordt over kegelsneden en hermitische krommen, gaan we dieper in op deze twee zaken. Op het einde behandelen we het affien vlak PG(2, q).
Het laatste deel is eenvoudiger: de lemma’s die we hier al dan niet voorzien van een bewijs, zijn nodig voor latere bewijzen vlot te laten verlopen.
De auteur maakt van dit moment ook het gebruik om mee te delen dat alle bewijzen en berekeningen doorheen dit hele werk zeer uitvoerig zijn neergeschreven. De reden hiervoor is dat dit de voorkeur van de auteur, als leerkracht, draagt.
1. Inleidende begrippen 1.1. Eindige velden
1.1
Eindige velden
1.1.1
Definities, notaties
(i) Een veld(
K
,+, ⋅) is een verzamelingK
gesloten onder de twee operaties+ en ⋅ zo dat (a) (K
,+) een abelse groep met eenheidselement 0 is;(b) (
K
∗,⋅) een abelse groep met eenheidselement 1 is (K
∗=K
\ {0});(c) Voor alle x, y, z∈
K
geldt er datx⋅ (y + z) = x ⋅ y + x ⋅ z,
(x + y) ⋅ z = x ⋅ z + y ⋅ z.
In het verloop van deze tekst noteren we x⋅ y als xy voor elke x, y ∈
K
.(ii) Voor elke element x∈
K
∗bestaat er een y∈K
∗zodat xy= 1 = yx. Het element y noemen we dan het invers element van x. We noteren dan y= x−1.(iii) Een eindig veld is een veld met een eindig aantal elementen.
(iv) De karakteristiek van een eindig veld
K
is het kleinste natuurlijk getal, en dus een priemgetal, p zo dat px= 0 voor elke x ∈K
.(v) GF(p) =
F
p, p priem, bestaat uit de restklassen modulo p met de natuurlijke optelling en de natuurlijke vermenigvuldiging. GF(p) is een eindig veld met p elementen.
(vi) Een eindig veld
K
van karakteristiek p heeft een deelveld isomorf met GF(p) en heeft phelementen,h≥ 1.
(vii) Als F(T) een irreduciebel polynoom van graad h over GF(p) is, dan
GF(ph) = GF(p)[T]/(F) = {a0+ a1t+ . . . + ah−1th−1∣ ai∈ GF(p), F (t) = 0} .
(viii) De elementen van x ∈ GF(q), q = ph voldoen aan de vergelijking Tq− T = 0. Er bestaat een
s∈ GF(q) zo dat
GF(q) = {0, 1, s, s2, . . . ,sq−2∣ sq−1 = 1} .
Deze s noemen we een primitief element of generator van GF(q). Dit heeft als gevolg dat voor elke x∈ GF(q)∗∶ xq−1 = 1.
(ix) Als s een generator van GF(q)∗is, dan is ook sr, r∈
Z
, een generator als en slechts als ggd(r, q−1) = 1.(x) Elk veld van q elementen is isomorf met GF(q) =
F
q.(xi) De additieve structuur van
F
qis gegeven door(F
q,+) ≅Z
p× . . . ×Z
p(h keer).(xii) De multiplicatieve structuur van
F
qis gegeven door(F
∗q,⋅) ≅Z
q−1.Lemma 1.1.1. Voor de elementen van
F
q, q> 2, geldt er met q − 1 ∤ i dat ∑x∈Fqx i= 0.Bewijs. Zij s een primitief element van
F
q. Dan krijgen we∑ x∈Fq xi= q−1 ∑ k=1 sik= q ∑ k=2 sik= q−1 ∑ k=1 si(k+1) = si q−1 ∑ k=1 sik.
Maar si≠ 1 (q − 1 is geen deler van i) en dus moet ∑x∈F qx
i= ∑q−1 k=1s
1. Inleidende begrippen 1.1. Eindige velden
Lemma 1.1.2. Het product van alle elementen uit
F
∗qis gelijk aan−1.Bewijs. Als voor x∈
F
∗qgeldt dat x−1 ≠ x, dan nemen we deze samen. Het product van deze twee is dansteeds 1. Maar welke elementen zijn dan wel gelijk aan hun inverse?
x−1 = x ⇔ x2= 1
⇔ x = ±1.
Zo ontstaat een product van een aantal keer 1 en één keer−1. Dit geeft ons het gewenste resultaat.
Lemma 1.1.3 (Freshman’s dream, I). Zij
F
een veld van karakteristiek p> 0 en veronderstel dat q = ph. Dan geldt voor alle elementen x, y∈F
(x + y)pi
= xpi
+ ypi
,
∀ i ∈ {1, 2, . . . , h}. In het bijzonder geldt er dus (x + y)q
= xq
+ yq
.
Bewijs. We starten met het geval i= 1 en ontwikkelen (x + y)pmet het binomium van Newton: (x + y)p= xp+ (p 1)x p−1 y+ . . . + ( p p− 1)xy p−1+ yp .
Voor elke i∈ {1, . . . , p − 1} hebben we dat (pi ) = p! i !(p − i)! = p (p − 1)! i !(p − i)! met i != 1 ⋅ 2 ⋅ . . . ⋅ i, (p − i)! = 1 ⋅ 2 ⋅ . . . ⋅ (p − i).
Elke factor van beide faculteiten is kleiner dan p. Omdat p priem is, zal geen enkele factor van i ! en (p − i)! een deler zijn van p. Met andere woorden
(pi ) =p⋅ ki,
voor een ki ∈
N
. Dus al deze coëfficiënten worden 0. Hierdoor verkrijgen we de gewenste gelijkheid.Neem nu een j zo dat 2≤ j ≤ h en veronderstel dat de gelijkheid geldt voor alle i < j. We tonen nu aan dat dit ook klopt voor j.
(x + y)pj = ((x + y)pj−1 ) p = (xpj−1 + ypj−1 ) p = (xpj−1 ) p + (ypj−1 ) p = xpj + ypj .
1.1.2
Morfismen
In dit deel samen met de volgende delen gaan we dieper in op afbeeldingen en in het bijzonder op morfismen, de spoorafbeelding en de Lagrange interpolatiepolynoom. We voorzien een bewijs waar we het nodig achten.
(i) Zij(
K
,+K,⋅K) en (L
,+L,⋅L) twee velden. Een afbeelding θ ∶K
→L
is een morfisme (of homomorfisme) als θ de structuur bewaart, i.e.
(k1+Kk2) θ= kθ 1+Lk θ 2, (k1⋅Kk2) θ = (k1) θ ⋅L(k2) θ voor alle k1en k2in
K
.1. Inleidende begrippen 1.1. Eindige velden
(ii) Als θ surjectief is, dan is het een epimorfisme. Indien θ injectief is, is het een monomorfisme. En
als θ een bijectie is, dan is het een isomorfisme.
(iii) Als θ een morfisme van
K
naar zichzelf is een endomorfisme. Een bijectief endomorfisme is eenautomorfisme.
(iv) De bovenstaande begrippen in het vet bestaan ook voor groepen. Normaal gezien zal het uit de
situatie duidelijk worden welke morfismen we gebruiken. Indien dat niet het geval is, zullen we de gepaste notatie gebruiken.
Lemma 1.1.4. In
F
q, q= 2h, is elk element een kwadraat. Dit betekent ook dat de afbeeldingenκ∶
F
q→F
q∶ x ↦ x 2 , κ−1 ∶F
q→F
q∶ x ↦ √ x, automorfismen zijn.Bewijs. Er geldt voor elke x, y∈
F
qdatx2= y2⇔ x2+ y2
⇔ (x + y)2= 0
⇔ x + y = 0 ⇔ x = y.
De afbeelding κ is dus injectief. Omdat
F
qeindig is, is κ ook surjectief en dus bijectief. We gaan nog nadat het een morfisme is. Kies x≠ y in
F
q.(x + y)2 = x2 + y2 , (xy)2 = x2 y2.
Bij de som maken we gebruik van de Freshman’s Dream. We besluiten dat κ een automorfisme is. De inverse afbeelding κ−1is bij gevolg ook een automorfisme.
Lemma 1.1.5. Er zijn juistq+12 kwadraten in
F
qmet q oneven. Een daarvan is het element 0.Bewijs. Beschouw de afbeelding κ∶
F
∗q→F
∗q∶ x ↦ x 2. Voor elke x en y in
F
∗qgeldt er datx2= y2⇔ (x − y)(x + y) = 0
⇔ x = ±y.
We vinden dus dat∣{x2∣ x ∈
F
∗q}∣ = 12∣F
∗q∣ en dus dat er q−12 + 1 = q+1
2 kwadraten zijn.
We sluiten dit deel af met het volgend lemma. Dit resultaat zal in hoofdstuk 2 van pas komen. Niet alle
Lemma 1.1.6. In
F
q, q oneven, zijn de volgende uitspraken equivalent.(i) ggd(q − 1, 4) = 2, (ii) q≡ −1 (mod 4),
(iii) −1 is een nietkwadraat in
F
q,(iv) x4= 1 heeft juist twee oplossingen in
F
q,1. Inleidende begrippen 1.1. Eindige velden
Bewijs. Omdat q oneven is, weten we dat q− 1 al zeker even is.
(i)⇔ (ii):
ggd(q − 1, 4) = 2 ⇔ 2∣(q − 1) ∧ 4 /∣ (q − 1) ⇔ ∃ m ∈
N
∶ q − 1 = 4m + 2 ⇔ ∃ m ∈N
∶ q = 4m + 3 ⇔ q ≡ −1 (mod 4) .(ii)⇔ (iii): De groep (
F
∗q,⋅) is cyclisch van grootte q − 1. Het element −1 is het enige element van dezegroep van orde 2. Omdat q oneven is, kan q≡ 0 (mod 4) of q ≡ 2 (mod 4) niet voorkomen. Dus de enige mogelijkheden zijn q≡ ε (mod 4) met ε ∈ {1, −1}. We tonen de contrapositie aan van de equivalentie die we willen bekomen.
∃ x ∈
F
∗ q∶ x 2 = −1 ⇔ x4 = 1 ⇔ 4∣q − 1 ⇔ q ≡ 1 (mod 4) .(iii)⇔ (iv): We weten dat x4= 1 al zeker twee oplossingen heeft: namelijk 1 en −1. Deze voldoen aan de vergelijking x2− 1 = 0. We krijgen dus dat
¬∃ x ∈
F
∗ q∶ x 2 = −1 ⇔ ¬∃ x ∈F
∗ q\{1, −1} ∶ x 4 = 1. (iv)⇒ (v): We nemen x ≠ y inF
∗q. x4= y4⇔ (xy )4= 1 ⇔ xy = ±1 ⇔ x = ±y.Dit betekent dat ∣{x4∣ x ∈
F
∗q}∣ = q−12 . Dit is juist dezelfde grootte van ∣{x 2
∣ x ∈
F
∗q}∣ (lemma 1.1.5).
Daarnaast geldt er dat {x4 ∣ x ∈
F
∗ q} ⊆ {x 4 ∣ x ∈F
∗ q}.Dus beide verzamelingen zijn gelijk of met andere woorden: de kwadraten in
F
q zijn juist de vierdemachten in
F
q.(v)⇒ (iii): We tellen eerst de grootte van de volgende verzameling
F
= {(x, x4) ∣ x ∈F
∗q}.Elke vierde macht x4is de vierde macht van x, maar ook van−x. Dit betekent dat x4de vierde macht is van tenminste 2 elementen van
F
∗q. Omdat de kwadraten juist de vierde machten zijn, weten we dat erjuistq−1
2 vierde machten in
F
∗qzijn. Zo krijgen we dat
∣
F
∣ ≥ q− 12 ⋅ 2 = q − 1. (1.1)
Elke x heeft natuurlijk een unieke vierde macht x4. Omdat∣
F
∗q∣ = q − 1 krijgen we dus dat ∣F
∣ = q − 1.We krijgen dus een gelijkheid in (1.1). Met andere woorden: elke vierde macht is de vierde macht van juist 2 elementen.
Zij nu x∈
F
∗q. Dan vinden we datx4= (x2)2, x4= (−x2)2.
Hierbij is x2het kwadraat van x en van−x. Maar x4is juist de vierde macht van deze twee. Dit betekent dat−x2geen oplossingen heeft. Wegens het feit dat x2een kwadraat is, is−1 dan geen kwadraat.
1. Inleidende begrippen 1.1. Eindige velden
1.1.3
Spoor
Zij
K
/F
een eindige velduitbreiding, waarbijF
=F
ρ,K
=F
ρm. Dan is het mogelijk om de volgende afbeelding, het spoor, te definiërentrK/F∶
K
→F
∶ x ↦ x + xρ+ xρ2
+ . . . + xρm−1
.
Lemma 1.1.7. De afbeelding trK/Fvoldoet aan de volgende eigenschappen. (i) ∀ x ∈
K
∶ trK/F(x) ∈F
.(ii) Het spoor is additief: ∀ x, y ∈
K
∶ trK/F(x + y) = trK/F(x) + trK/F(y). (iii) ∀ x ∈K
,∀ k ∈F
∶ trK/F(kx) ∶ k ⋅ trK/F(x).(iv) ∀ k ∈
F
∶ trK/F(k) = hk. (v) ∀ x ∈K
∶ trK/F(xρ) = trK/F(x).(vi) Zij
L
een eindige velduitbreiding vanK
, dan is het spoor transitief:∀ x ∈
L
∶ trL/F(x) = trK/F(trL/K(x)) . (1.2)In het bijzondere geval dat
F
=F
penK
=F
q, q= p h, passen we de notatie aan:
trp∶
F
q→F
p∶ x ↦ x + x p+ xp2
+ . . . + xph−1
.
Als p= 2, dan hebben we
tr∶
F
q→F
2∶ x ↦ x + x 2+ x4
+ . . . + x2h−1 .
Voor elke x∈
F
qgeldt er dat x 2h= xq
= x. Op deze manier kunnen we tot volgende vaststelling komen.
tr(x2) + tr (x) = x2+ x4+ x8+ . . . + x2 h + x + x2 + x4 + . . . + x2h−1 = x + 2x2+ 2x4+ . . . + 2x2h−1+ x2h = 0. (1.3)
Bijgevolg is tr(x) ∈ {0, 1} voor elke x ∈
F
q. Zo kunnen we twee verzamelingen definiëren:T
0= {x ∈F
q∣ tr (x) = 0} ,T
1= {x ∈F
q∣ tr (x) = 1} .Lemma 1.1.8. De verzamelingen
T
0enT
1voldoen aan de volgende eigenschappen. (i) 0∈T
0; (ii) 1∈ {T
0, als q= 2 2m ,T
1, als q= 2 2m+1;(iii) t∈
T
i⇒ tγ∈T
i, voor elk automorfisme γ vanF
q;(iv) s∈
T
i, t∈T
j ⇒ s + t ∈ {T
0, als i= j,
T
1, als i≠ j; (v) ∣T
0∣ = ∣T
1∣ = q2.1. Inleidende begrippen 1.1. Eindige velden
1.1.4 Functies
In dit werk gebruiken we volgende notatie
G
[T] = {F ∈F
q[T] ∣ deg(F) ≤ q − 1} .Lemma 1.1.9. Elke functie f ∶
F
q →F
q is gedefinieerd door een polynoom F ∈G
[T]. Meer bepaald,f(x) = F (x) waarbij F(T) = − ∑ s∈Fq f(s)T q− T T− s . (1.4)
Bewijs. Kies een vaste s∈
F
q. We bekijken dan de overeenkomstige term van de som:f(s)T q − T T− s = f (s) ∏ x∈Fq\{s} T− x. (1.5)
(i) Als we T= s invullen, dan wordt (1.5) het volgende: f(s) ∏
v∈Fq\{s}
s− v = f (s) ∏
v′∈F∗q
v′= −f (s).
Als v varieert over
F
q\{s}, dan zal s − v = v′variëren overF
∗q. Tenslotte gebruiken we lemma 1.1.2voor de laatste overgang.
(ii) Als we T= u invullen met u ≠ s, dan wordt (1.5) het volgende: f(s) ∏
v∈Fq\{s}
u− v = 0.
We verkrijgen 0 omdat één van deze factoren u− u zal zijn.
Deze werkwijze kunnen we voor elke s∈
F
qdoen. Zo wordt (1.4) dan voor een x∈F
qdanF(x) = − (−f (x)) = f (x).
Gevolg 1.1.10. Indien f∶
F
q→F
qeen permutatie is, dan is de graad van F, gedefinieerd zoals in lemma1.1.9, hoogstens q− 2.
Bewijs. Zij deze f een permutatie. We werken het linkerlid van (1.4) uit:
− ∑ s∈Fq f(s) (Tq−1+ aq−2Tq−2+ . . .) =⎡⎢⎢⎢⎢⎢⎢ ⎢⎣− ∑s∈Fq f(s)⎤⎥⎥⎥⎥⎥⎥ ⎥⎦T q−1+ L.O.T. =⎡⎢⎢⎢⎢⎢⎢ ⎢⎣− ∑s∈Fq s⎤⎥⎥⎥⎥⎥⎥ ⎥⎦T q−1+ L.O.T.
Omdat f een permutatie is, mogen we deze laatste gelijkheid toepassen. Maar wegens lemma 1.1.1 is de coëfficiënt van Tq−1 gelijk aan 0.
Definitie 1.1.11. Een element F∈
G
[T], waarvoor de corresponderende functie f een permutatie is,wordt een permutatiepolynoom genoemd. We noteren daarnaast
P
(q; T) = {F ∈G
[T] ∣ F is een permutatiepolynoom} .In hoofdstuk 2 zal het nodig zijn om aan te tonen dat bepaalde polynomen geen permutatiepolynomen zijn. Om dat te kunnen bewijzen, hebben we volgend lemma (en in het bijzonder zijn gevolg) nodig.
1. Inleidende begrippen 1.1. Eindige velden
Lemma 1.1.12. Als F ∈
G
[T], dan F ∈P
(q; T) als en slechts als beide voorwaarden tegelijk voldaanzijn:
(i) voor elke r/≡ 0 (mod p) en r ≤ q − 2, is de graad van F (T)rmodulo Tq− T ten hoogste q − 2; (ii) F(x) = 0 heeft juist één oplossing in
F
q.Gevolg 1.1.13. Als F∈
G
[T], met F (0) = 0 en q = 2h, dan F∈P
(q; T) als en slechts als beide voorwaar den tegelijk voldaan zijn:(i) voor elke oneven r en r≤ q − 2, de graad van F (T)r modulo Tq− T ten hoogste q − 2 is; (ii) F(x) = 0 impliceert dat x = 0.
1.1.5
Vergelijkingen en wortels
In dit werk zullen we vaak werken met een kwadratische vergelijking over
F
q, q= p h, i.e.
aT2+ bT + c = 0, (1.6)
met a, b en c in
F
qen a≠ 0. We sommen kort de verschillende gevallen omtrent het aantal oplosingenop:
Indien p≠ 2, dan kunnen we de discriminant, Δ = b2− 4ac, bepalen. ⋄ Als Δ = 0, dan heeft (1.6) de unieke oplossing t = −b2a.
⋄ Als Δ geen kwadraat is, dan heeft (1.6) geen oplossingen. ⋄ Als Δ = s2
voor een s∈
F
∗q, dan heeft (1.6) twee oplossingen, nl. t= −b±s2a .Indien p= 2, dan is het niet mogelijk om met Δ te werken. ⋄ Indien b = 0, dan heeft (1.6) de unieke oplossing t =√c
a.
⋄ Als b ≠ 0, dan worden volgende substituties toegepast
Y= aT b , δ=ac
b2.
Zo kunnen we (1.6) schrijven als
aT2+ bT + c = 0 ⇔ a2T2+ abT + ac = 0 ⇔ a 2 b2T 2 + a bT+ ac b2 = 0 ⇔ Y2 + Y + δ = 0. (1.7)
De constante δ noemen we de Sinvariant van vergelijking (1.6) en van vergelijking (1.7). Wegens (1.3), weten we dat tr(δ) ∈ {0, 1}.
◦ Als tr (δ) = 1, dan heeft (1.7) en dus (1.6) geen oplossingen.
◦ Als tr (δ) = 0, dan heeft (1.7) en dus (1.6) twee oplossingen. Neem hiervoor een k ∈
F
qwaarvoor tr(k) = 1 en definieer y= h−1 ∑ i=2 δi⋅⎡⎢⎢⎢⎢⎢⎢ ⎢⎣ i−1 ∑ j=1 kj⎤⎥⎥⎥⎥⎥⎥ ⎥⎦.
1. Inleidende begrippen 1.1. Eindige velden
Dan zal y2+ y = δ en dan zal y een oplossing van (1.7) zijn. Dit heeft als gevolg dat y + 1 de tweede oplossing van (1.7) is:
(y + 1)2
+ (y + 1) = y2
+ 1 + y + 1 = y2
+ y = δ.
We eindigen dit deel met een lemma over de vergelijking Tn= c. Hier geven we geen bewijs, omdat het niet van groot belang is in het vervolg van dit werk.
Lemma 1.1.14. Zij c∈
F
q, q= p h. De vergelijking Tn = c heeft een unieke oplossing wanneer er geldt dat ggd(n, q − 1) = 1. Deze unieke oplossing is x = crwaar r∈
Z
, r∈Z
en nr+ r′(q − 1) = 1.1. Inleidende begrippen 1.2. Projectieve ruimten
1.2
Projectieve ruimten
Het volgende deel in dit hoofdstuk behandelt de projectieve ruimten. Ook hier zullen we enkele zaken gewoon oplijsten in de veronderstelling dat de lezer al bekend is met deze begrippen en concepten.
1.2.1
Definities
(i) Zij V= V(n+1, q) een (n+1)dimensionale vectorruimte over een veld
K
. Beschouw de equivalentie over de elementen van V∗= V\ {0}. Zij ¯x = (x0,x1, . . . ,xn) en ¯y = (y0,y1, . . . ,yn) ∈ V∗, dan¯
x∼ ¯y ⇔ ∃ t ∈
K
∗∶ (tx0,tx1, . . . ,txn) = (y0,y1, . . . ,yn).De equivalentieklassen zijn dan de ééndimensionale deelruimten van V, zonder nul. De verzamel ing D(V) van deze equivalentieklassen is dan de ndimensionale projectieve ruimte over
K
. Deze wordt genoteerd als PG(n,K
) of PG(V).(ii) Indien
K
=F
q, dan gebruiken we de notatie PG(n, q).(iii) De projectieve dimensie of meetkundige dimensie van PG(n,
K
) of PG(n, q) is n.(iv) De elementen van PG(n,
K
) noemen we punten. Zij P een willekeurig punt in PG(n,K
). Dit puntstelt een ééndimensionale deelruimte van V voor. Kies een vector ¯x ∈ P\ {0}. Ten opzichte van
een basis{¯e0, ¯e1, . . . , ¯en} van V is ¯x = (x0,x1, . . . ,xn). Dan noemt men (x0,x1, . . . ,xn) de homo
gene coördinaten van het punt P en is ¯x een representant van P. Ten opzichte van de gekozen
basis zijn de homogene coördinaten van P op een factor t∈
K
∗ na bepaald. We noteren P(¯x) ofP(x0,x1, . . . ,xn) om duidelijk te maken wat de homogene coördinaten van het punt P zijn.
(v) De punten P(¯x1), . . ., P (¯xr) zijn lineair onafhankelijk als een verzameling vectoren ¯x1, . . ., ¯xrlineair
onafhankelijk zijn.
(vi) Voor m∈ {−1, 0, 1, 2, . . . , n} is een mdimensionale deelruimte van PG(n,
K
) een verzameling vanpunten waarvan de representanten, samen met de nulvector, een(m + 1)dimensionale deelruimte van V vormen. We zeggen dan dat U meetkundige dimensie m heeft en noteren dit als mdim(U) =
m.
(vii) Als U een deelruimte van V is, noteren we dat U≤ V. Analoog betekent W ≤ PG(n,
K
) dat W eendeelruimte van PG(n,
K
) is.(viii) De deelruimten van dimensie 0 zijn de punten, terwijl de deelruimte van dimensie −1 de ledige
verzameling is. Deelruimten van dimensie 1, 2 en 3 noemen we respectievelijk rechten, vlakken en solids. Indien een deelruimte dimensie n− 1 heeft, dan is het een hypervlak.
(ix) Indien n= 2, dan spreken we over een projectief vlak in plaats van een projectieve ruimte. Hierin
gelden volgende eigenschappen:
(a) Door elke twee verschillende punten gaat er een unieke rechte; (b) Elke twee verschillende rechten snijden elkaar in een uniek punt; (c) PG(2,
F
) bevat vier punten, waarvan geen drie collineair zijn.(x) Zij
P
= (P, R, I) een drietal bestaande uit de verzameling P van punten, de verzameling R vanrechten en een incidentierelatie I die voldoet (a), (b) en (c) van (ix). Dan noemt men
P
een axiomatisch projectief vlak. Indien P en R eindig zijn, dan zegt men dat het projectief vlak eindig is.
In dat geval bestaat er een natuurlijk getal m∈
N
\ {0, 1} waarvoor ∣P∣ = ∣R∣ = m2+ m + 1.Dat getal m noemt men de orde van het projectief vlak. Het aantal rechten door een punt is dan
1. Inleidende begrippen 1.2. Projectieve ruimten
(xi) Indien
F
=F
q, dan spreken we van het projectief vlak PG(2, q), waarbij q juist de orde is. Hierondergeven we twee voorbeelden.
(xii) Is PG(V) een projectief vlak over een veld
F
met P de verzameling der punten, R de verzameling der rechten en I de inclusie, dan isP
= (P, R, I) een axiomatisch projectief vlak.(xiii) We merken echter op een axiomatisch projectief vlak op andere manieren kan geconstrueerd wor
den, waarbij niet vertrokken wordt van een vectorruimte. Het resulterend projectief vlak is dan niet isomorf met een projectief vlak afkomstig van een vectorruimte.
Voorbeeld 1.2.1. Het projectief vlak van orde 2, PG(2, 2), heeft 22+ 2 + 1 = 7 rechten en 7 punten.
Daarnaast gaan er 2+ 1 = 3 rechten door elk punt. Analoog liggen er 3 punten op elke rechte.
Figuur 1.1: Het projectief vlak PG(2, 2).
Het vlak PG(2, 2) wordt ook het Fanovlak genoemd. Dit is het projectief vlak met het kleinste aantal punten en rechten. De tekening van dit vlak is vrij eenvoudig. Het wordt al wat moeilijker om een overzichtelijke tekening te maken van het vlak PG(2, 3).
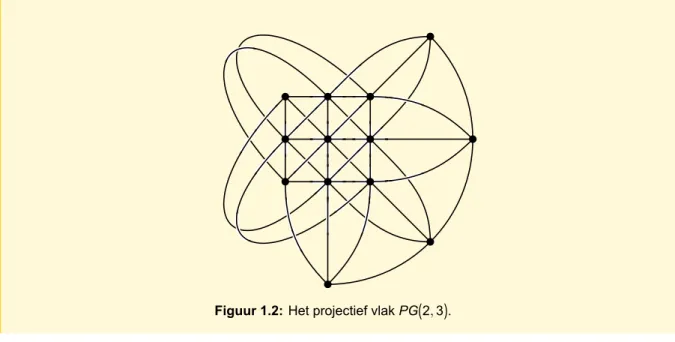
Voorbeeld 1.2.2. Het vlak PG(2, 3) heeft 32+ 3 + 1 = 13 rechten en 13 punten. Er gaan 3 + 1 = 4
rechten door elk punt en er liggen 4 punten op elke rechte.
Figuur 1.2: Het projectief vlak PG(2, 3).
Tenslotte vermelden we nog de stelling van Desargues. In PG(V), dim(V) = 3, is deze stelling waar. Een projectief vlak waar deze stelling waar is, noemen we een desarguesiaans. We merken op dat er vele eindige en oneindige nietdesarguesiaanse vlakken bestaan.
1. Inleidende begrippen 1.2. Projectieve ruimten
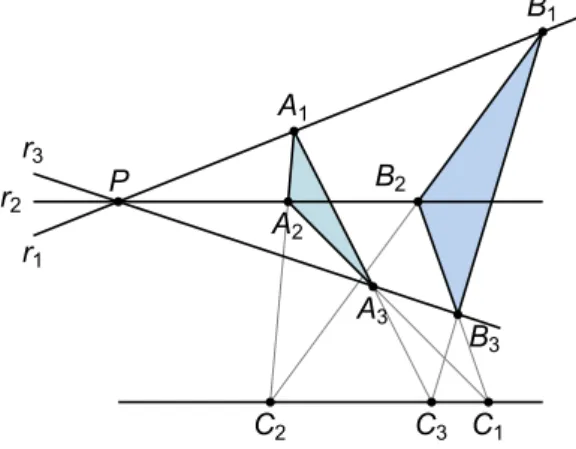
Lemma 1.2.3 (Stelling van Desargues). Kies een punt P∈ PG(V), dim(V) = 3, en drie verschillende
rechten r1, r2en r3in PG(V) die door P gaan. Kies op de rechte ri, 1≤ i ≤ 3, twee punten Aien Bizodat
P, Aien Bionderling verschillend zijn. Onderstel dat de punten A1, A2en A3niet collineair zijn, net zoals de punten B1, B2en B3. Dan zijn de punten C1= A1A2∩ B1B2, C2= A1A3∩ B1B3en C3= A2A3∩ B2B3 collineair. r3 r2 r1 P A1 A2 A3 B1 B2 B3 C1 C2 C3
Figuur 1.3: Tekening horende bij lemma 1.2.3.
1.2.2
Karakterisering van deelruimten
In dit korte deel sommen we een karakterisering voor deelruimten op. Vervolgens bekijken we het bij zondere geval voor hypervlakken. Dit bijzondere geval wordt dan bekeken in PG(2, q), samen met diens duale situatie.
Lemma 1.2.4. Als
M
een deelverzameling punten van PG(n, q) is, zo dat het een nietledige doorsnede heeft met elke mdimensionale ruimte, dan∣
M
∣ ≥ qn−r+1− 1
q− 1 . (1.8)
De gelijkheid in (1.8) wordt bereikt als en slechts als
M
een(n − m)dimensionale ruimte is.Gevolg 1.2.5. Als
M
een deelverzameling punten van PG(n, q) is, zo dat het een nietledige doorsnede heeft met elke rechte, dan∣
M
∣ ≥ qn− 1
q− 1. (1.9)
De gelijkheid in (1.9) wordt bereikt als en slechts als
M
een hypervlak is.Gevolg 1.2.6. Als
M
een deelverzameling punten van PG(2, q) is, zo dat elke rechte een punt vanM
bevat, dan∣
M
∣ ≥ q2− 1
q− 1 = q + 1. (1.10)
De gelijkheid in (1.10) wordt bereikt als en slechts als
M
een rechte is.Gevolg 1.2.7. Het duale van gevolg 1.2.6 is het volgende. Als
M
een deelverzameling rechten van PG(2, q) is, zo dat elk punt op een rechte vanM
ligt, dan∣
M
∣ ≥ q2− 1
q− 1 = q + 1. (1.11)
1. Inleidende begrippen 1.2. Projectieve ruimten
1.2.3
Polariteiten en perspectiviteiten
(i) Neem twee vectorruimten V en W over isomorfe velden
F
enF
′. Is φ een afbeelding van V in W en θ een isomorfisme vanF
opF
′, waarvoor voldaan is aan(a) (¯x1+ ¯x2) φ = ¯xφ 1+ ¯x φ 2,∀ ¯x1, ¯x2∈ V; (b) (k¯v)φ= kθ¯vφ,∀ k ∈
F
,∀ ¯v ∈ V;dan is φ een semilineaire afbeelding van V in W met corresponderend isomorfisme θ. Indien
F
=F
′ en θ= id, dan is φ een lineaire afbeelding van V in W. Is φ een bijectie, dan spreken we van eennietsinguliere semilineaire afbeelding en nietsinguliere lineaire afbeelding.
(ii) Zij V een vectorruimte over het veld
K
, dim(V) ≥ 2. Dan stelt men de groep van nietsinguliere semilineaire afbeeldingen van V op zichzelf voor door ΓL(V). De deelgroep van ΓL(V) bestaande uit de nietsinguliere lineaire afbeeldingen van V op zichzelf wordt genoteerd als GL(V) en wordt de algemene lineaire groep van V genoemd.(iii) Zij V en W twee vectorruimten over respectievelijke velden
K
enK
′, dim(V) ≥ 3 en dim(W) ≥ 3. Een collineatie of isomorfisme van PG(V) op PG(W) is een bijectieγ∶ PG(V) → PG(W) ∶ ∀ U1,U2≤ V ∶ U1⊂ U2⇒ U γ 1 ⊂ U
γ 2.
(iv) Een correlatie of antiisomorfisme van PG(V) op PG(W) is een bijectie γ∶ PG(V) → PG(W) ∶ ∀ U1,U2≤ V ∶ U1⊂ U2⇒ U
γ 2 ⊂ U
γ 1.
(v) Indien PG(V) = PG(W) spreken we een automorfisme en antiautomorfisme in plaats van respec
tievelijk collineatie en correlatie. Een automorfisme γ met γ2 = 1 is een involutie, terwijl een anti automorfisme γ met γ2= 1 een polariteit is.
(vi) Ten opzichte van de gekozen basis van V kan de polariteit γ van PG(V) steeds voorgesteld worden
door ⎛ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜⎜ ⎝ a0 a1 ⋮ an ⎞ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎟⎟⎟ ⎠ = A ⋅ ⎛ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜⎜ ⎝ xθ0 xθ1 ⋮ xθn ⎞ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎟⎟⎟ ⎠ ,
met θ2= id en A een nietsinguliere (n + 1) × (n + 1)matrix over
F
qwaarvoor{A
T∈ {A, −A}, θ = 1,
ATθ= A, θ2= id, θ ≠ id.
(vii) Een polariteit zal een punt P(x0,x1, . . . ,xn) afbeelden op een hypervlak met vergelijking
a0X0+ a1X1+ . . . + anXn= 0.
In PG(2, q) is het hypervlak een rechte L, die we ook de poollijn noemen. We noteren dan dat
L= pγ. In het bijzondere geval het punt op zijn corresponderend hypervlak ligt, wordt dat punt een
absoluut punt van de polariteit γ genoemd. (viii) We hebben de volgende polariteiten.
(a) Indien q oneven is, dan zijn er de volgende polariteiten.
⋄ Is n oneven en AT= −A en θ = id, dan spreken we van een symplectische polariteit γ s.
⋄ Is AT = A en θ = id, dan spreekt men van een orthogonale polariteit γ o.
1. Inleidende begrippen 1.2. Projectieve ruimten
⋄ Is θ2= id en θ ≠ id, dan spreekt met van een hermitische polariteit γ h.
(b) Indien q even is, dan zijn er de volgende polariteiten.
⋄ Is n oneven en AT= −A en θ = id en zijn alle diagonaalelementen gelijk aan 0, dan spreekt
men over een symplectische polariteit γs. ⋄ Is AT
= A en θ = id en zijn niet alle diagonaalelementen gelijk aan 0, dan spreekt men over een pseudo polariteit γp.
⋄ Is θ2= id en θ ≠ id, dan spreekt met van een hermitische polariteit γ h.
(ix) Voor elke polariteit is het mogelijk om ten opzichte van een goedgekozen basis in V de polariteit
voor te stellen door de volgende matrix A. We zullen ons beperken tot polariteiten in PG(2, q). (a) Voor een symplectische polariteit γs:
A=⎛⎜⎜ ⎝ 0 1 0 −1 0 0 0 0 0 ⎞ ⎟⎟ ⎠.
(b) Voor een orthogonale polariteit γo of hermitische polariteit γhis A een diagonaalmatrix met coëfficiënten van
F
qdie voldoet aan Aθ
= A. (c) Voor een pseudo polariteit γp:
A=⎛⎜⎜ ⎝ 1 0 0 0 0 1 0 1 0 ⎞ ⎟⎟ ⎠.
(x) We geven het aantal absolute punten van de polariteiten in PG(2, q) mee. Aangezien n = 2 even
is, zullen we geen symplectische polariteiten hebben.
(a) Bij een orthogonale polariteit γois de verzameling van de absolute punten een nietsinguliere kegelsnede. (Zie deel 1.2.4)
(b) Bij een pseudo polariteit γp kan ten opzichte van een goedgekozen basis de unie van de
absolute punten voorgesteld worden door de rechte X0= 0. Dus heeft γpjuist q+ 1 collineaire
absolute punten.
(c) Bij een hermitische polariteit γh, met q een kwadraat, vormen de absolute punten een hermi tische variëteit. (Zie deel 1.2.5)
(xi) De Fundamentaalstelling van de Projectieve Meetkunde geeft ons dit gevolg.
Onderstel dat V een vectorruimte, dim(V) ≥ 3, over een veld
K
is. Dan wordt de groep van alle automorfismen van de projectieve meetkunde PG(V) geïnduceerd door de groep van alle nietsinguliere semilineaire afbeeldingen van V op zichzelf.(xii) De groep van alle automorfismen van PG(V) op zichzelf, geïnduceerd door de elementen van ΓL(V), noteren we als PΓL(V). De projectieve groep van PG(V) is de groep van alle collineaties
van PG(V) op zichzelf, geïnduceerd door de elementen van GL(V).
(xiii) Twee deelverzamelingen U1 en U2van PG(V) worden projectief equivalent genoemd als er een
element γ∈ PGL(V) bestaat zodat Uγ1= U2. We noteren dan dat U1≅ U2.
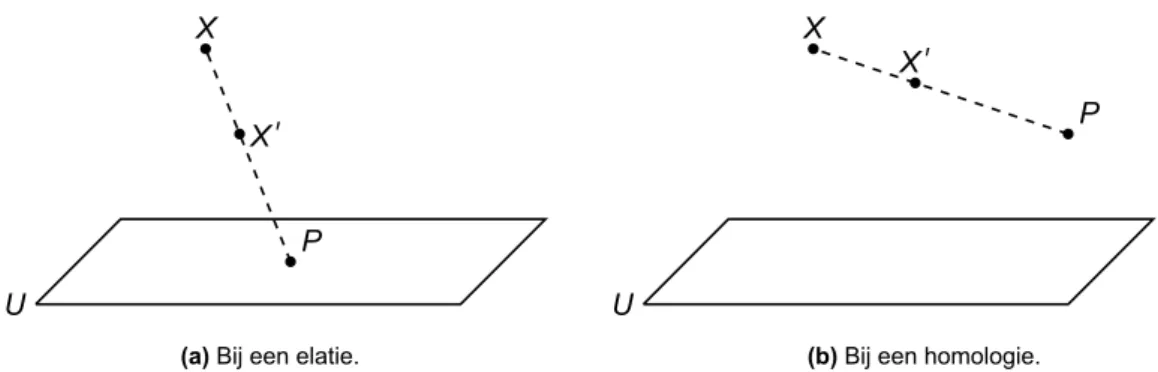
(xiv) Een perspectiviteit is een element van PΓL(V) die alle punten van een hypervlak U fixeert. U wordt
dan de as genoemd. Een punt P wordt het centrum genoemd als de perspectiviteit elk hypervlak door P fixeert. Dit centrum is steeds uniek.
(xv) Een niettriviale perspectiviteit noemt men een elatie al het centrum op de as ligt. Indien dit niet
het geval is, spreken we van een homologie.
Lemma 1.2.8. Gegeven zijn een punt P en een hypervlak U. Zijn X, X′punten die verschillend zijn van P, die niet op U gelegen zijn en die zodanig gelegen zijn dat P, X en X′collineair zijn. Dan bestaat er juist één perspectiviteit γ met as U en centrum P waarvoor Xγ= X′.
1. Inleidende begrippen 1.2. Projectieve ruimten
U
P X
X′
(a) Bij een elatie.
U
P X
X′
(b) Bij een homologie.
Figuur 1.4: Tekening horende bij lemma 1.2.8.
1.2.4
Kegelsneden
Doorheen dit werk zal er vaak gebruik gemaakt worden van kegelsneden in PG(2, q). Daarom sommen we in dit deel enkele begrippen, stellingen en eigenschappen omtrent kegelsneden op.
(i) Elke verzameling
C
van punten in PG(2, q) waarvan de homogene coördinaten (x0,x1,x2) voldoenaan een vergelijking van de vorm
F(X0,X1,X2) = a00X 2 0 + a11X 2 1+ a22X 2 2+ a01X0X1+ a02X0X2+ a12X1X2= 0,
met niet alle coëfficiënten aij∈
F
qgelijk aan nul, noemen wij een kegelsnede.(ii) Het kwadratisch polynoom F(X0,X1,X2) wordt absoluut reduciebel genoemd als deze in een bepaalde
extensie van
F
q te schrijven is als een product van lineaire factoren. Als dit niet mogelijk is, isF(X0,X1,X2) absoluut irreduciebel. We zeggen dan ook dat
C
absoluut irreduciebel als dezebeschreven wordt door een vergelijking F(X0,X1,X2) = 0 waarbij F (X0,X1,X2) een absoluut ir
rediciebel kwadratisch polynoom is.
(iii) Indien q oneven is, kunnen we
C
ook voorstellen aan de hand van een matrixA= ⎛ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎝ a00 a01 2 a02 2 a01 2 a11 a12 2 a02 2 a12 2 a22 ⎞ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎠ .
Men kan aantonen dat F(X0,X1,X2) absoluut reduciebel is als en slechts als A singulier is. Indien A nietsingulier is, dan is
C
de verzameling van absolute punten van de orthogonale polariteit γodie met A correspondeert.
(iv) Indien q even is, zal het niet mogelijk zijn om een matrix A op te stellen. Er geldt wel dat F(X0,X1,X2)
absoluut reduciebel is als en slechts als
a00a 2 12+ a11a 2 02+ a22a 2 01+ a01a02a12= 0.
De bovenstaande gelijkheid is equivalent met zeggen dat het punt(a12,a02,a01) tot de kegelsnede
behoort. Het punt met(a12,a02,a01) noemen we ook de kern van de kegelsnede. Ook als F niet
absoluut reduciebel is, spreken we van de kern.
(v) Als
C
absoluut reduciebel is, dan isC
één van de volgende verzamelingen. ⋄ De verzameling punten van twee verschillende rechten,⋄ de verzameling punten van één rechte, ⋄ een singleton.
1. Inleidende begrippen 1.2. Projectieve ruimten
(vi) Indien
C
een nietledige absoluut irreduciebele kegelsnede in PG(2, q), q oneven, is, dan de basis in V(3, q) zo gekozen worden datC
kan voorgesteld worden door X12= X0X2, ofC
= {(1, t, t2)∣ t ∈F
q} ∪ {(0, 0, 1)} .
Hierbij geldt dat∣
C
∣ = q + 1 en de bijhorende matrix is danA= ⎛ ⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜ ⎝ 0 0 −1 2 0 1 0 −1 2 0 0 ⎞ ⎟⎟⎟⎟ ⎟⎟⎟⎟ ⎟⎟ ⎠ .
(vii) We spreken bij kegelsneden ook over de volgende rechten en punten. Er worden ook enkele
aantallen meegegeven.
(a) Een externe rechte van een kegelsnede
C
in PG(2, q) is een rechte die geen punt vanC
bevat. (b) Een raaklijn van een kegelsnedeC
in PG(2, q) is een rechte die één punt vanC
bevat. (c) Een snijlijn van een kegelsnedeC
in PG(2, q) is een rechte die twee punten vanC
bevat. (d) ZijC
een absoluut irreduciebele kegelsnede in PG(2, q) met q oneven. Een intern punt is eenpunt waarvan de poollijn ten opzichte van
C
een externe rechte is. Een extern punt is een punt waarvan de poollijn ten opzichte vanC
een snijlijn is.(e) Er zijn in totaal (q−1)q2 externe rechten (en dus evenveel interne punten), q+ 1 raaklijnen en
(q+1)q
2 snijlijnen (en dus evenveel externe punten).
(f) Er gaan 2 raaklijnen, q−12 snijlijnen en q−12 externe rechten door een extern punt. (g) Er gaan 0 raaklijnen, q+12 snijlijnen en q+12 externe rechten door een intern punt. (h) Er liggen q+12 interne punten en q+12 externe punten op een externe rechte.
(i) Er liggen q−1
2 interne punten en q−1
2 externe punten op een snijlijn.
Lemma 1.2.9. Beschouw 5 verschillende punten van PG(2, q) waarvan er geen 3 collineair zijn. Dan is
er juist één kegelsnede die deze 5 punten bevat.
Bewijs. Omdat geen drie van deze punten collineair zijn, kunnen we het coördinatenstelsel zo kiezen
dat P1= (1, 0, 0), P2= (0, 1, 0), P3= (0, 0, 1), P4 = (1, 1, 1) en P5= (1, ε, η) zijn, met ε en η ∈
F
q. Omdater geen 3 van deze punten collineair zijn, kunnen we het volgende over P5zeggen.
⋄ Als ε = 0, dan P5= (1, 0, η) ∈ P1P3. Als ε= 1, dan P5= (1, 1, η) ∈ P3P4. Beiden zijn strijdig met het
gegeven.
⋄ Als η = 0, dan P5 = (1, ε, 0) ∈ P1P2. Als η = 1, dan P5 = (1, ε, 1) ∈ P2P4. Ook deze twee gevallen
zorgen voor een strijdigheid.
⋄ Als ε = η, dan P5= (1, ε, ε) ∈ P1P4Dit zorgt ook voor een strijdigheid.
Dus P5= (1, ε, η) met η ≠ η ∈
F
q\{0, 1}. We drukken nu uit dat deze 5 punten op de kegelsnedeC
∶ a00X 2 0 + a11X 2 1 + a22X 2 2 + a01X0X1+ a02X0X2+ a12X1X2= 0 liggen.⋄ De punten P1, P2en P3geven ons dat a00= a11= a22= 0.
⋄ P4∈
C
zorgt ervoor dat a01+ a02+ a12= 0.⋄ Het punt P5tenslotte zorgt dat a01ε+ a02η+ a12εη= 0.
De enige kegelsnede die hieraan voldoet is
1. Inleidende begrippen 1.2. Projectieve ruimten
1.2.5
Hermitische krommen
(i) Een hermitische kromme
K
van PG(2, q2), n ≥ 1, is elke verzameling punten van PG(2, q2) methomogene coördinaten die voldoen aan de vergelijking van de vorm
F(X0,X1,X2) = X q+1 0 + X q+1 1 + X q+1 2 ,
met het corresponderend automorfisme θ∶
F
q2→F
q2∶ x ↦ xq.(ii) Zij γheen hermitische polariteit van PG(2, q2). Dan vormen de absolute punten van γheen hermi tische kromme.
(iii) Voor elke rechte r in PG(2, q2), geldt er dat ∣r ∩
K
∣ ∈ {1, q + 1}. (iv) ZijK
een hermitische kromme in PG(2, q2).(a)
K
heeft in totaal q3+ 1 punten.(b) Er zijn in totaal q3+ 1 raaklijnen en het aantal (q + 1)secanten is juist q4− q3+ q2. (c) Zij P∈
K
. Dan behoort P tot 1 raaklijn en q2verschillende(q + 1)secanten.(d) Zij Q∉
K
. Dan gaan er q+ 1 raaklijnen en q2− q verschillende (q + 1)secanten door Q.Lemma 1.2.10. Zij
K
een Hermitische kromme in PG(2, q2). Zij Q een punt niet opK
. Dan zijn de q+ 1 snijpunten vanK
met de q+ 1 raaklijnen door Q collineair: ze behoren allen tot de poollijn Qγh.Bewijs. Zij γh de hermitische polariteit zo dat de absolute punten van γh juist
K
vormen. Dan hebben we voor elke raaklijn r door Q datQ∈ r = (r ∩
K
)γh ⇒ Qγh ∋ rγh = ((r ∩K
)γh)γh = r ∩K
.
Opmerking. In dit bovenstaande lemma maken we geen gebruik van het feit dat we met een hermit
ische polariteit werken. Het enige wat we gebruiken, zijn de eigenschappen van polariteiten. Het is dus mogelijk om gelijkaardige stellingen te bewijzen voor alle polariteiten.
1.2.6
Het affien vlak AG(2,q)
(i) Beschouw een rechte L in PG(2, q). Dan is AG(2, q) = PG(2, q)\L een affiene ruimte van dimensie 2 of affien vlak over
F
q.(ii) De deelruimtes van AG(2, q) zijn juist de deelruimtes van PG(2, q), maar met de punten L verwij
derd.
(iii) De rechte L noemt men de rechte op oneindig en wordt vaak genoteerd als L∞.
(iv) Door de rechte met vergelijking X2 = 0 als L∞ te kiezen, kunnen we alle punten van AG(2, q)
noteren als(x0,x1,1) of korter als (x0,x1). De punten van AG(2, q) zijn juist de punten van V(2, q). (v) Drie punten X= (x0,x1), Y = (y0,y1) en Z = (z0,z1) in AG(2, q) zijn collineair als en slechts als er
een λ∈
F
q\{0, 1} bestaat zo datX= λY + (1 − λ)Z. (1.12)
(vi) Een andere representatie van AG(2, q) gaat als volgt. Beschouw de bijectie ψ∶ AG(2, q) →
F
q2 ∶ X = (x0,x1) ↦ x = x0+ x1α,1. Inleidende begrippen 1.2. Projectieve ruimten
Lemma 1.2.11. Drie verschillende punten X= (x0,x1), Y = (y0,y1) en Z = (z0,z1) in AG(2, q) zijn collineair als en slechts als
(x − y)q−1 = (x − z)q−1,
met x= ψ(X), y = ψ(Y) en z = ψ(Z) in
F
q2.Bewijs.
⇒: Als X, Y en Z collineair zijn, dan bestaat er een λ ∈
F
q\{0, 1} zo dat X = λY + (1 − λ)Z. InF
q2 wordt ditx= λy + (1 − λ)z ⇒ λx − λx + x = λy + (1 − λ)z ⇒ λx + (1 − λ)x = λy + (1 − λ)z ⇒ λ(x − y) = (1 − λ)(z − x) ⇒ λ(x − y) = (λ − 1)(x − z) ⇒ λq−1(x − y)q−1= (λ − 1)q−1(x − z)q−1 ⇒ (x − y)q−1= (x − z)q−1 .
De laatste overgang bekomen we door het feit dat λ en λ− 1 tot
F
∗qbehoren.⇐: Zij (x − y)q−1= (x − z)q−1, dan
(xx− y− z)q−1= 1 ⇒ xx− y− z = λ, (1.13)
voor een λ∈
F
q\{0}. Kan het dat λ = 1? Indien dat zo zou zijn, dan is x − y = x − z en dus y = z. Maar X,Y en Z zijn verschillend en ψ is een bijectie, zodat x, y en z ook verschillend zijn. Dus λ∈
F
q\{0, 1}. Degelijkheid rechts van de pijl in (1.13) leidt tot
x− y
x− z = λ ⇒ x − y = λx − λz
⇒ x − λx = y − λz ⇒ y = (1 − λ)x + λz.
1. Inleidende begrippen 1.3. Getaltheorie
1.3
Getaltheorie
1.3.1
Grootste gemeenschappelijke deler
Lemma 1.3.1. Veronderstel dat a, b∈
Z
(niet beiden nul) en dat d = ggd(a, b). Dan bestaan x, y ∈Z
zodanig dat ax+ by = d, tenzij b een deler is van a.Lemma 1.3.2. Zij n∈
N
en h∈N
. Dan geldt er dat ggd(2n− 1, 2h− 1) = 2ggd(n,h)− 1.Bewijs. Zij k= ggd(n, h) dan k = nx + hy voor een x ∈
Z
en een y∈Z
(lemma 1.3.1). Als d= ggd(2n− 1, 2h− 1) dan ∃ a ∈Z
∶ ad = 2n− 1 ⇒ 2n≡ 1 (mod d) , ∃ b ∈Z
∶ bd = 2h − 1 ⇒ 2h ≡ 1 (mod d) , ⇒2k= 2nx+hy= (2n)x(2h)y≡ 1 (mod d) ⇒2k− 1 = cd, c ∈Z
⇒d∣2k − 1.Anderzijds, wegens k∣m, is 2k− 1∣2n− 1 en analoog zal 2k− 1∣2n− 1. Met andere woorden, 2k− 1 is een gemeenschappelijke factor en dus een deler van d. We komen tot de conclusie dat
ggd(2n− 1, 2h− 1) = d = 2k− 1 = 2ggd(n,h)− 1.
1.3.2
Lineaire congruenties
Zij m∈
N
en beschouwZ
/mZ
, de verzameling van de restklassen modulo m.Definitie 1.3.3. Een element r∈
Z
/mZ
wordt inverteerbaar genoemd als er een element y∈Z
/mZ
bestaat zodanig dat ry= 1 inZ
/mZ
, of met andere woorden als ry≡ 1 (mod m). We noteren hetinvers element y van r als r−1.
Lemma 1.3.4. Een element r∈
Z
/mZ
is inverteerbaar als en slechts als r en m onderling ondeelbaar zijn. In het bijzonder is inZ
/pZ
, p een priemgetal, elk element verschillend van 0 inverteerbaar.Definitie 1.3.5. Een vergelijking van de vorm
ax≡ b (mod m) ,
met a, b∈
Z
gegeven gehele getallen en x een onbekende inZ
/mZ
, wordt een lineaire congruentie genoemd.Het oplossen van zo’n lineaire congruentie is equivalent met het zoeken naar een koppel(x, t), x ∈
N
,x< m en t ∈
Z
zodat ax= b + mt.Lemma 1.3.6.
(i) Als d = ggd(a, m) geen deler van b is, dan bezit de lineaire congruentie ax ≡ b (mod m) geen oplossing.
1. Inleidende begrippen 1.3. Getaltheorie
(ii) Als d = ggd(a, m) een deler van b is, dan bezit de lineaire congruentie ax ≡ b (mod m) juist d oplossingen r met r∈
N
en r< m.Bewijs.
(i) Veronderstel dat ggd(a, m) = d > 1 geen deler is van b. Indien r ∈
N
en r< m een oplossing is van de lineaire congruentie ax≡ b (mod m), dan bestaat er een geheel getal k zodanig dat ar − b = km of dus dat ar− km = b. Hieruit zou volgen dat d een deler is van b. Een tegenstrijdigheid.(ii) Veronderstel dat ggd(a, m) = 1 of met andere woorden: a en m zijn onderling ondeelbaar. Dan
volgt uit lemma 1.3.4 dat a inverteerbaar is in
Z
/mZ
. Dit betekent dat er een element a−1 ∈Z
/mZ
bestaat zodat a−1a≡ 1 (mod m). Zo krijgen we al data−1(ax) ≡ (a−1b) (mod m) ,
of dus x≡ a−1b (mod m). Dit is de unieke oplossing van de lineaire congruentie.
Als ggd(a, m) = d > 1 een deler is van b, dan kunnen we beide leden van de lineaire congruentie delen door d. a dx≡ b d (mod m d) , ggd(a d, m d) = 1.
Hierdoor zitten we opnieuw in de vorige situatie. De laatste lineaire congruentie bezit juist één oplossing r∈
N
met r<m d of dus a dr− b d = k m d ⇒ ar = b + km.Beschouw nu r+ tmd met t∈
N
en t< md. Dan vinden we, met ad= g, data(r + tm
d) = ar + at m
d = b + km + gtm ≡ b (mod m) .
We krijgen juist d oplossingen.
1.3.3
Stelling van Lucas
De laatste belangrijke stelling is bekend onder de naam Lucas’s theorem. De Franse wiskundige E. Lucas publiceerde dit voor het eerst in het jaar 1878. Een populair bewijs van N.J. Fine maakt gebruik van de Freshman’s dream om deze stelling te bewijzen [14].
Lemma 1.3.7 (Freshman’s dream, II). Zij p een priemgetal en i> 0. Dan geldt er dat
(x + y)pi ≡ xpi + ypi (mod p) . In het bijzonder is(1 + x)p i = 1 + xpi .
Bewijs. Het bewijs verloopt analoog zoals in lemma 1.1.3.
Lemma 1.3.8 (Lucas’ theorem). Voor twee natuurlijke getallen m, n en een priemgetal p geldt er vol
gende gelijkheid (mn ) = k ∏ i=0 (mi ni) (mod p) ,
1. Inleidende begrippen 1.3. Getaltheorie waarbij m= k ∑ i=0 mip i , n= k ∑ i=0 nip i ,
met 0≤ mi< p en 0 ≤ ni< p voor alle i ∈ {0, 1, 2, . . . , k}. Indien m < n, dan (mn) = 0.
Bewijs. (1 + x)m= (1 + x)∑ki=0mip i = k ∏ i=0 ((1 + x)pi)mi≡∏k i=0 (1 + xpi)mi (mod p) .
We gaan op zoek naar de coëfficiënt van xnin(1 + x)m. In het linkerlid is dat juist(mn). Voor het rechterlid betekent dit dat we de coëfficiënt van
xn0⋅ (xp)n1⋅ . . . ⋅ (xp k ) nk = k ∏ i=0 (xpi)ni
zoeken. De coëfficiënt van zo’n factor(xp j
)nj, 0 ≤ j ≤ k, vinden we terug in de biomiale uitbreiding van (1 + xpj)nj en is dus(mj nj). Zo bekomen we dat (mn ) ≡ k ∏ i=0 (mi ni) (mod p) .
Als mi< ni, dan(mnii) = 0 en dus (mn) ≡ 0 (mod p).
Opmerking. Het is ook mogelijk om Lucas’ theorem aan de hand van inductie te bewijzen.
Gevolg 1.3.9 (Bijzonder geval van Lucas’ theorem). Zij 2k− 1 en n met k, n ∈
N
en n< 2k− 1. Dan(2
k− 1
n ) = 1 (mod 2) .
Bewijs. We bekijken eerst 2k− 1. Aangezien we weten dat
2k− 1 = 20+ 21+ 22+ . . . + 2k−1=
k−1
∑
i=0
2i,
krijgen we dat mi = 1 voor elke i. Analoog veronderstellen we
n= k−1 ∑ i=0 ni2 i ,
met ni∈ {0, 1}. Wegens lemma 1.3.8 weten we dus dat
(2 k − 1 n ) = k−1 ∏ i=0 (n1 i) = 1.
Deze laatste overgang komt uit de twee volgende vaststellingen. (11) =1, (1
2
K-bogen van graad 2
In dit hoofdstuk bestuderen we de kbogen van graad 2. Hiervoor zijn verschillende bronnen gebruikt, waaronder het boek van J.W.P. Hirschfeld [16] het meest frequent geraadpleegd werd. Andere werken, zoals van M. Brown [7] en B. De Bruyn [9], zorgden voor een waardevolle aanvulling.
Allereerst voeren we de definitie van een kboog in, samen met de enkele definities betreffende de rechten in het vlak PG(2, q). We vinden al vlug een bovengrens voor de grootte van een kboog. Deze geven ons de kans om verschillende tellingen uit te voeren: eerst voor de bisecanten, dan voor de raaklijnen en tenslotte voor de externe rechten. We proberen deze zo uitvoerig en zo duidelijk mogelijk neer te schrijven. Sommige tellingen zijn voorzien van een kleine tekening ter ondersteuning.
In het daaropvolgende stuk bespreken we het aantal punten op een khoek en het aantal khoeken in
PG(2, q). Hierbij zal 1 ≤ k ≤ 5. De reden dat we deze tellingen doen, is omdat er een verband tussen kbogen en khoeken zit: de verzameling toppen van een khoek is een kboog. De resultaten die we
dus vinden, zullen later van nut zijn.
Daarna bekijken we de ovalen en de hyperovalen. Dat zijn juist de kbogen waar de bovengrens van de grootte bereikt wordt. Eerst geven we enkele resultaten omtrent de rechten (bisecanten, raaklijnen en externe rechten). Vervolgens bespreken we de Stelling van Segre: elke(q + 1)boog (m.a.w. een ovaal) is een nietontaarde kegelsnede. Dit resultaat klopt voor q oneven. Voor q even geldt dit enkel als q∈ {2, 4}.
Uiteindelijk gaan we dieper in op de hyperovalen. Eerst bekijken we de hyperovalen die bepaald worden door een opolynoom F(T). Indien F (T) = Trvoor een r∈
N
, krijgen we enkele interessante resultaten. Een tweede klasse is deze van de translatiehyperovalen. Met behulp van enkele resultaten uit de vorige klasse hyperovalen, zullen we ook hier een mooi resultaat vinden. Daarna wijken we even uit naarPG(3, q). De reden hiervoor is dat L. Storme en J.A.F. Thas een verband gevonden hebben tussen
hyperovalen in PG(2, q), q even en partiële flocks op een kwadriek
Q
in PG(3, q), q even. Dit omvangrijke deel over hyperovalen sluiten we af met een synthese over de andere klasses.Het laatste grote stuk van dit hoofdstuk gaat over complete bogen. We vinden enkele voorwaarden opdat een kboog niet compleet zou zijn. Vervolgens bekijken we of er complete bogen bestaan verschillend van (hyper)ovalen. Met behulp van enkele constructies en Sage kunnen we hier een antwoord op bieden.
2. Kbogen van graad 2 2.1. Een kboog van graad 2
2.1
Een k-boog van graad 2
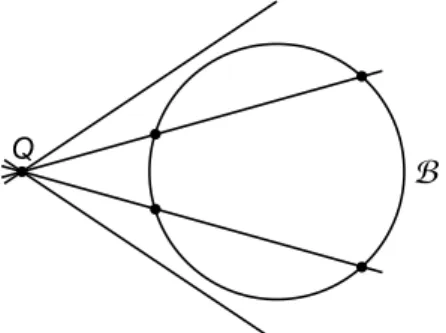
Definitie 2.1.1. Een kboog
B
van graad 2 in PG(2, q) is een verzameling van k punten (k ≥ 3) zo dat geen 3 punten vanB
collineair zijn. Met andere woorden: elke rechte snijdtB
in ten hoogste 2 punten.De rechten in PG(2, q) krijgen specifieke namen naargelang hun doorsnede met
B
. Aangezien elke rechte hoogstens twee punten vanB
kan bevatten, krijgen we drie mogelijke doorsneden.Definitie 2.1.2. Zij
B
een kboog en r een willekeurige rechte in PG(2, q).(i) Als∣r ∩
B
∣ = 0, dan is r een 0secant of externe rechte. (ii) Als∣r ∩B
∣ = 1, dan is r een 1secant of raaklijn. (iii) Als∣r ∩B
∣ = 2, dan is r een 2secant of bisecant.Soms is het mogelijk om een bestaande kboog uit te breiden naar een(k + 1)boog. Dit zorgt voor de volgende notaties en begrippen.
Definitie 2.1.3. Zij een kboog
B
in PG(2, q).(i) Een punt P∈ PG(2, q) breidt
B
uit naar een(k + 1)boog a.s.a.B
∪ {P} een (k + 1)boog is. (ii)B
is compleet alsB
niet bevat is in een(k + 1)boog. Anders noemen weB
niet compleet. (iii) Het maximum aantal punten die een kboogB
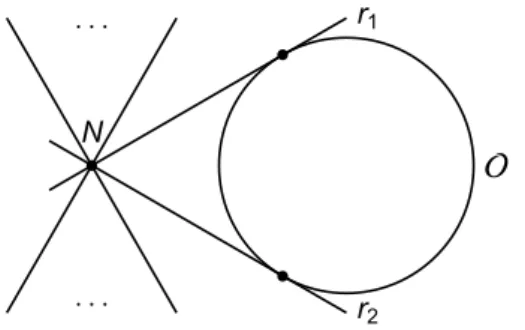
kan hebben, noteren we als m(2, q). Daarbij kunnen we ons de volgende vraag stellen.“Wat is de maximale grootte van een kboog van graad 2?”
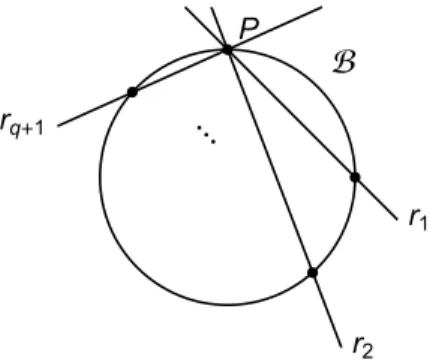
Stelling 2.1.4. In PG(2, q) geldt er dat
m(2, q) = {q+ 2, q even, q+ 1, q oneven.
Bewijs. Zij
B
een willekeurige kboog in PG(2, q). We kiezen een willekeurig punt P ∈B
. Door dit punt gaan q+ 1 rechten: r1, r2, . . ., rq+1. Elke rechte ri, 1≤ i ≤ q + 1, is ofwel een raaklijn ofwel een bisecant.Dus kan elke rinog hoogstens één ander punt van
B
bevatten. Dan geldt er dat k≤ 1 + (q + 1) = q + 2.B
P
r1
r2 rq+1 ⋱