Naslagwerk deel 9
Grafostatica
Uitgave 2016-1 AuteurHC
hugoclaeys@icloud.comInhoudsopgave
1 Inleiding 7
2 Samenstellen en ontbinden van krachten 8
2.1 Samenstellen van twee krachten waarvan de werklijnen elkaar snijden . . . 8
2.1.1 Opgave . . . 8
2.1.2 Twee krachten samenstellen door middel van een parallellogram . . . 9
2.1.3 Twee krachten samenstellen door middel van een krachtendriehoek . . . . 10
2.2 Ontbinden van een kracht in twee componenten waarvan de werklijnen elkaar snijden 10 2.2.1 Voorbeeld 1 . . . 10
2.2.2 Voorbeeld 2 . . . 11
2.3 Samenstellen van meerdere krachten waarvan de werklijnen elkaar snijden in één punt 12 2.4 Samenstellen van meerdere krachten waarvan de werklijnen niet door één punt gaan 13 2.4.1 Voorbeeld 1 . . . 13
2.4.2 Voorbeeld 2 . . . 15
2.5 Ontbinden van een kracht in drie componenten waarvan de werklijnen gegeven zijn 16 2.6 Samenstellen van twee krachten waarvan de werklijnen elkaar buiten de tekening snijden . . . 16
2.7 Elementen van poolfiguur en stangenveelhoek . . . 19
2.8 Samenstellen van meerdere krachten waarvan de werklijnen elkaar buiten de tekening snijden . . . 20
2.9 Bepalen van de resultante van evenwijdige krachten . . . 22
3 Evenwicht van krachten 25 3.1 Balk ondersteund in twee punten . . . 25
3.2 Spant . . . 26
3.3 Driescharnierspant . . . 28
3.3.1 Driescharnierspant voorbeeld 1 . . . 29
3.3.2 Driescharnierspant voorbeeld 2 . . . 31
3.4 Vakwerk . . . 33
3.5 Steunpunt reactiekrachten van belaste liggers . . . 35
3.5.1 Voorbeeld 1: ligger belast met puntlasten . . . 35
3.5.3 Voorbeeld 3: ligger belast met puntlasten en gelijkmatige lasten . . . 40
3.5.4 Voorbeeld 4: ligger belast met schuine puntlasten . . . 41
4 Zwaartepunt van een vlakke figuur 45 5 Momenten- en dwarskrachtenlijn 48 5.1 Inleiding . . . 48
5.2 Het moment van een evenwijdige krachten ten opzichte van een punt . . . 48
5.3 In de einden ondersteunde balk met puntlasten . . . 50
5.4 In twee punten ondersteunde balk met overstekende einden en puntlasten . . . . 52
5.5 In de einden ondersteunde balk met puntlasten en gelijkmatige belasting . . . 54
5.6 Balk met enkel een gelijkmatige belasting . . . 56
6 Vakwerken 59 6.1 Inleiding . . . 59
6.2 Staafkrachten in een ligger . . . 59
6.3 Het Cremona-diagram . . . 62
6.4 Kraan oplossen met knooppunten methode . . . 63
6.5 Kraan oplossen met Cremona-diagram . . . 64
6.6 Luifel . . . 66
6.7 Vakwerkligger van een brug oplossen met Cremona-diagram . . . 69
6.8 Dakspant oplossen met Cremona-diagram . . . 72
6.9 Brugligger met zijdelingse belasting . . . 73
6.10 De snedenmethodes van Culmann . . . 76
7 Invloedslijn en uiterste waarden 79 7.1 Inleiding . . . 79
Lijst van figuren
2.1 Samenstellen van twee krachten . . . 8
2.2 Samenstellen van twee krachten met parallellogram: de werklijnen . . . 9
2.3 Samenstellen van twee krachten met parallellogram: de resultante . . . 9
2.4 Samenstellen van twee krachten methode 2 . . . 10
2.5 Ontbinden van een kracht in twee componenten . . . 11
2.6 Krachten in een bok . . . 12
2.7 Samenstellen van krachten die elkaar snijden in één punt: voorbeeld 1 . . . . 12
2.8 Samenstellen van krachten die elkaar snijden in één punt: voorbeeld 2 . . . . 13
2.9 Samenstellen van krachten die elkaar niet in één punt snijden: opgave . . . . 14
2.10 Samenstellen van krachten die elkaar niet in één punt snijden: stap 1 . . . 14
2.11 Samenstellen van krachten die elkaar niet in één punt snijden: stap 2 . . . 15
2.12 Samenstellen van krachten die elkaar niet snijden in één punt . . . 15
2.13 Twee krachten snijden buiten het blad: opgave . . . 16
2.14 Twee krachten snijden buiten het blad: krachtendriehoek . . . 17
2.15 Twee krachten snijden buiten het blad: poolfiguur . . . 17
2.16 Twee krachten snijden buiten het blad: stangenveelhoek . . . 18
2.17 Twee krachten snijden buiten het blad: resultante . . . 19
2.18 Meerdere krachten snijden buiten het blad: opgave . . . 20
2.19 Meerdere krachten snijden buiten het blad: krachtenveelhoek . . . 20
2.20 Meerdere krachten snijden buiten het blad: poolfiguur . . . 21
2.21 Meerdere krachten snijden buiten het blad: stangenveelhoek . . . 21
2.22 Meerdere krachten snijden buiten het blad: resultante . . . 22
2.23 Evenwijdige krachten: opgave . . . 22
2.24 Evenwijdige krachten: krachtenveelhoek . . . 23
2.25 Evenwijdige krachten: poolfiguur . . . 23
2.26 Evenwijdige krachten: stangenveelhoek . . . 24
2.27 Evenwijdige krachten: resultante . . . 24
3.1 Balk ondersteund in uiteinden en belast met puntlast: opgave . . . 25
3.2 Balk ondersteund in uiteinden en belast met puntlast: oplossing . . . 26
3.3 Spant: opgave . . . 27
3.5 Spant: de reactiekrachten in de steunpunten . . . 28 3.6 Driescharnierspant 1: opgave . . . 29 3.7 Driescharnierspant 1: stap 1 . . . 29 3.8 Driescharnierspant 1: stap 2 . . . 30 3.9 Driescharnierspant 1: stap 3 . . . 30 3.10 Driescharnierspant 2: opgave . . . 31 3.11 Driescharnierspant 2: stap 1 . . . 31 3.12 Driescharnierspant 2: stap 2 . . . 32 3.13 Driescharnierspant 2: stap 3 . . . 33 3.14 Vakwerk 1: opgave . . . 33 3.15 Vakwerk 1: krachtenveelhoek . . . 34 3.16 Vakwerk 1: poolfiguur . . . 34 3.17 Vakwerk 1: stangenveelhoek . . . 34
3.18 Ligger belast met puntlasten: opgave . . . 35
3.19 Ligger belast met puntlasten: poolfiguur . . . 35
3.20 Ligger belast met puntlasten: stangenveelhoek en resultante . . . 36
3.21 Ligger belast met puntlasten: stangenveelhoek en reactiekrachten . . . 36
3.22 Ligger belast met puntlasten: poolfiguur en reactiekrachten . . . 37
3.23 Ligger belast met puntlasten: reactiekrachten . . . 37
3.24 Ligger belast met puntlasten: opgave . . . 38
3.25 Ligger belast met puntlasten: poolfiguur . . . 38
3.26 Ligger belast met puntlasten: stangenveelhoek . . . 39
3.27 Ligger belast met puntlasten: reactiekrachten . . . 39
3.28 Ligger belast met puntlasten en gelijkmatige last: opgave . . . 40
3.29 Ligger belast met puntlasten en gelijkmatige last: poolfiguur . . . 40
3.30 Ligger belast met puntlasten en gelijkmatige last: stangenveelhoek . . . 41
3.31 Ligger belast met puntlasten en gelijkmatige last: reactiekrachten . . . 41
3.32 Ligger belast met schuine puntlasten: opgave . . . 42
3.33 Ligger belast met schuine puntlasten: poolfiguur . . . 42
3.34 Ligger belast met schuine puntlasten: stangenveelhoek . . . 43
3.35 Ligger belast met schuine puntlasten: reactiekrachten . . . 44
4.1 Zwaartepunt van een vlakke figuur: opgave . . . 45
4.2 Zwaartepunt van een vlakke figuur: stap 1 . . . 46
4.3 Zwaartepunt van een vlakke figuur: stap 2 . . . 47
5.1 Het moment van evenwijdige krachten ten opzichte van een punt . . . 49
5.2 In de einden ondersteunde balk met puntlasten: opgave . . . 50
5.3 In de einden ondersteunde balk met puntlasten: stap 1 . . . 50
5.6 In twee punten ondersteunde balk met overstekende einden en puntlasten: opgave 52 5.7 In twee punten ondersteunde balk met overstekende einden en puntlasten: stap 1 52 5.8 In twee punten ondersteunde balk met overstekende einden en puntlasten: stap 2 53 5.9 In twee punten ondersteunde balk met overstekende einden en puntlasten: stap 3 54 5.10 In de einden ondersteunde balk met puntlasten en gelijkmatige belasting: opgave 54 5.11 In de einden ondersteunde balk met puntlasten en gelijkmatige belasting: stap 1 55 5.12 In de einden ondersteunde balk met puntlasten en gelijkmatige belasting: stap 2 56
5.13 Balk met gelijkmatige belasting: opgave . . . 56
5.14 Balk met gelijkmatige belasting: reactiekrachten . . . 57
5.15 Balk met gelijkmatige belasting: dwarskrachten . . . 57
5.16 Balk met gelijkmatige belasting: buigend moment . . . 58
6.1 Staafkrachten in een ligger: opgave . . . 60
6.2 Staafkrachten in een ligger: de reactiekrachten . . . 60
6.3 Staafkrachten in een ligger: krachten in de knooppunten . . . 61
6.4 Staafkrachten in een ligger: stap 3 . . . 61
6.5 Cremona-diagram . . . 62
6.6 Kraan: opgave . . . 63
6.7 Kraan: knooppunten methode . . . 64
6.8 Kraan: Cremona-diagram . . . 65
6.9 Luifel: opgave . . . 66
6.10 Luifel: reactiekrachten . . . 67
6.11 Luifel: uitwendige krachtenveelhoek . . . 68
6.12 Luifel: Cremona-diagram . . . 69
6.13 Brugligger: opgave . . . 69
6.14 Brug: uitwendige krachtenveelhoek . . . 70
6.15 Brug: Cremona-diagram knooppunt 1 . . . 71
6.16 Brug: Cremona-diagram tot het midden van de ligger . . . 71
6.17 Dakspant: opgave . . . 72
6.18 Dakspant: uitwendige krachtenveelhoek . . . 72
6.19 Dakspant: Cremona-diagram . . . 73
6.20 Brugligger met zijdelingse belasting: opgave . . . 74
6.21 Brugligger met zijdelings belasting: steunpunt reactiekrachten . . . 74
6.22 Brugligger met zijdelingse belasting: Cremona-diagram . . . 75
6.23 Staafkrachten met methode Culmann: opgave . . . 76
6.24 Staafkrachten met methode Culmann: snede a . . . 77
6.25 Staafkrachten met methode Culmann: snede b . . . 78
6.26 Staafkrachten met methode Culmann: snede c . . . 78
7.1 Invloedslijn ten gevolge van een puntlast: opgave . . . 79
7.3 Invloedslijn dwarskracht ten gevolge van een puntlast . . . 80 7.4 Invloedslijn buigend moment ten gevolge van een puntlast . . . 81
Hoofdstuk 1
Inleiding
Grafostatica houdt zich bezig met het grafisch oplossen van evenwichtsvraagstukken. Ik zie grafostatica als een aanvulling op de analytische methode (de sterkteleer). Het voordeel van de grafostatica is dat het de probleemstelling grafische voorstelt en oplost.
De elementen die we in dit naslagwerk steeds zullen tegenkomen zijn krachten. Een kracht is een vectorgrootheid die gekenmerkt wordt door haar grootte, richting en zin.
• De richting wordt weergegeven door de werklijn van de kracht.
• De grootte is bepaald door de lengte van het lijnstuk.
• De zin geven we aan met een pijl.
• Tot slot is er nog het aangrijpingspunt.
Het spreekt vanzelf dat we alles op schaal tekenen. Op een tekening kunnen we meerdere schalen tegenkomen want elke grootheid kan zijn eigen schaal hebben (denk aan kracht, lengte, moment ...).
Het tekenen gebeurde in mijn studententijd (rond 1970) op papier met behulp van een goed uitgeruste tekentafel. Vandaag doe ik het op de computer met behulp van een teken- of CAD programma.
Opmerking:
Noteer dat omwille van leesbaarheid van de tekeningen het vectorsymbool (het pijltje) boven de vector ontbreekt.
Hoofdstuk 2
Samenstellen en ontbinden van
krachten
2.1
Samenstellen van twee krachten waarvan de werklijnen
el-kaar snijden
2.1.1 Opgave
In figuur 2.1 heb ik twee krachten ~F1 en ~F2 getekend. Onze opdracht: bepaal de resultante ~R van deze twee krachten.
10 kN
F1
F2
Figuur 2.1: Samenstellen van twee krachten
Er zijn twee methodes om dit probleem grafisch op te lossen:
2.1.2 Twee krachten samenstellen door middel van een parallellogram Ik leg de methode met de parallellogram in een drie stappen uit.
1. In een eerste stap teken ik de werklijnen van de beide krachten. Belangrijk is het snijpunt S van de twee werklijnen (zie figuur 2.2).
S
10 kN
F1
F2
Figuur 2.2: Samenstellen van twee krachten met parallellogram: de werklijnen
2. In een tweede stap verschuif ik de beide krachten langs hun werklijn totdat de oorsprong van beide krachten samenvallen met het snijpunt S (zie figuur 2.3). De verschoven krachten noem ik ~F10 en ~F20.
3. Tenslotte teken ik een parallellogram met als zijden de verschoven krachten. De resultante ~R is de diagonaal van de parallellogram die vertrekt in de oorsprong van de beide krachten (zie figuur 2.3).
R F2' F1' 10 kN F1 F2 S
2.1.3 Twee krachten samenstellen door middel van een krachtendriehoek De oplossing bestaat uit de volgende stappen (zie figuur 2.4):
1. Teken de werklijnen van de krachten en bepaal het snijpunt.
2. Verschuif één kracht ( ~F1 in mijn voorbeeld) langs haar werklijn totdat haar oorsprong samenvalt met het snijpunt van de werklijnen. De nieuwe vector is ~F10.
3. Teken vanaf het eindpunt van ~F10 een vector parallel, even groot en met dezelfde zin als de vector van de tweede kracht ~F2. Deze nieuwe vector is ~F20.
4. Teken tenslotte een vector die begint bij het beginpunt van ~F10 en eindigt bij het eindpunt van ~F20. Deze vector ~R is de resultante. De drie vectoren vormen een driehoek, vandaar krachtendriehoek. R F2' F1' 10 kN F1 F2
Figuur 2.4: Samenstellen van twee krachten methode 2
2.2
Ontbinden van een kracht in twee componenten waarvan
de werklijnen elkaar snijden
Ik ga dit onderwerp behandelen aan de hand van twee voorbeelden. Noteer dat in mijn tekeningen zowel de krachten als de afstanden op schaal getekend zijn.
2.2.1 Voorbeeld 1
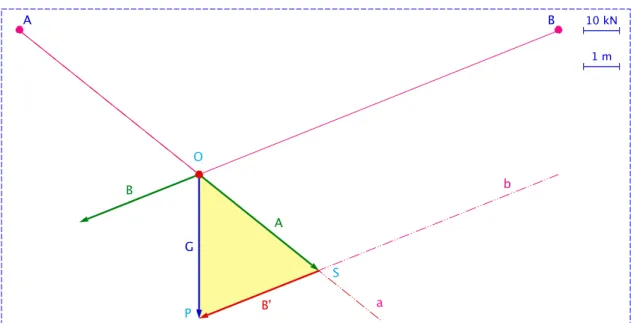
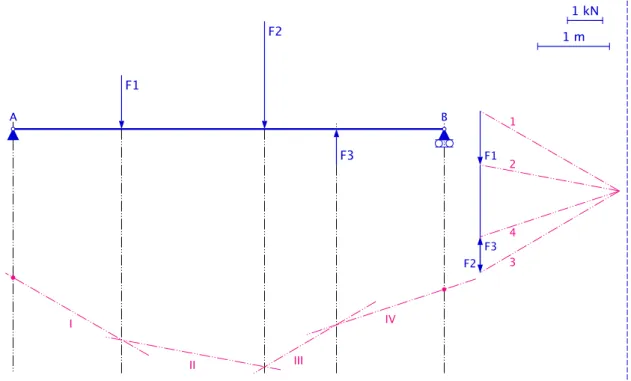
• Gegeven: zie figuur 2.5. Een kabel is bevestigd aan de punten A en B. In het punt O is er een gewicht ~G aan de kabel bevestigd. Het gewicht veroorzaakt in de beide kabeldelen AO en BO een kracht.
G A B 10 kN 1 m A B' B O P S a b
Figuur 2.5: Ontbinden van een kracht in twee componenten
• Oplossing:
1. AO en BO zijn de werklijnen van de gezochte krachten.
2. Teken de werklijn b evenwijdig met BO en die door P het eindpunt van ~G gaat.
3. De werklijnen a en b snijden elkaar in S.
4. De driehoek OSP is de krachtendriehoek. We hebben ~G gesplitst in de vectoren ~A en ~B0.
5. Teken vanaf het snijpunt O de vector ~B parallel, even groot en met dezelfde zin als de vector ~B0.
6. In het kabeldeel AO heerst er een kracht ~A.
7. In het kabeldeel BO heerst er een kracht ~B.
2.2.2 Voorbeeld 2
• Gegeven: zie figuur 2.6. In het punt A van een bok werkt de kracht ~F loodrecht naar beneden. De grootte van ~F is 200 kN.
• Gevraagd: Bepaal de krachten in de boom AB en de trekstang AC.
• Oplossing:
1. AB en AC zijn de werklijnen van de gezochte krachten.
3. Deze lijnen vormen een parallellogram met ~F als diagonaal.
4. Beide zijden van het parallellogram zijn de gezochte krachten.
5. In de trekstang AC heerst de trekkracht ~F1. Rekening houdend de schaal is de trekkracht 127 kN.
6. In de boom AB heerst er de drukkracht ~F2. Rekening houdend de schaal is de drukkracht 289 kN. 100 kN F 1 m C B A F2 F1
Figuur 2.6: Krachten in een bok
2.3
Samenstellen van meerdere krachten waarvan de werklijnen
elkaar snijden in één punt
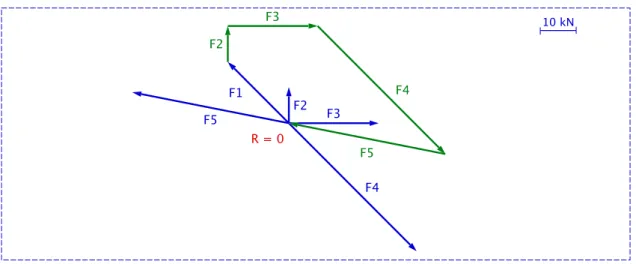
10 kN F1 F2 F3 F4 O F2 F3 F4 R
Ik behandel dit onderwerp aan de hand van twee voorbeelden. Zie resp. figuur 2.7 en 2.8. De oplossing gebeurt telkens door middel van het construeren van een krachtenveelhoek. De resultante is de vector die het beginpunt van de eerste vector verbindt met het eindpunt van de laatste vector. We noemen deze lijn de sluitlijn van de krachtenveelhoek.
10 kN F1 F2 F5 F3 F4 F2 F3 F4 F5 R = 0
Figuur 2.8: Samenstellen van krachten die elkaar snijden in één punt: voorbeeld 2
In het geval van figuur 2.8 is er geen sluitlijn omdat het eindpunt van de laatste vector samenvalt met het beginpunt van de eerste vector. De resultante is hier ’nul’. De krachten maken hier evenwicht (de krachtenveelhoek is gesloten).
2.4
Samenstellen van meerdere krachten waarvan de werklijnen
niet door één punt gaan
Ik ga dit onderwerp behandelen aan de hand van twee voorbeelden.
2.4.1 Voorbeeld 1
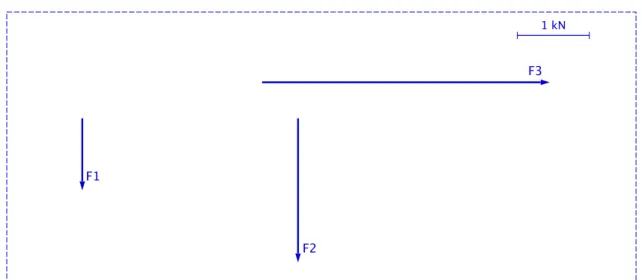
Figuur 2.9 stelt de opgave van ons eerste probleem voor.
Om dit probleem op te lossen ga ik als volgt tewerk:
1. Ik teken de werklijnen a en c van resp. de krachten ~F1 en ~F3. De werklijnen snijden elkaar in het punt O (zie figuur 2.10).
2. Ik verschuif beide krachten langs hun werklijn totdat hun begin samenvalt met O.
3. Nu teken ik een parallellogram met ~F1 en ~F3 als zijde. De diagonaal is de resultante ~R1 van beide krachten.
1 kN
F1
F2
F3
Figuur 2.9: Samenstellen van krachten die elkaar niet in één punt snijden: opgave
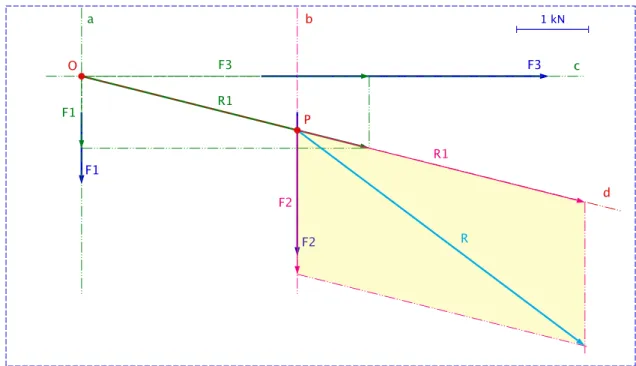
1 kN F1 F2 F3 R1 F3 F1 a c O
Figuur 2.10: Samenstellen van krachten die elkaar niet in één punt snijden: stap 1
4. Ik teken de werklijnen b en d van resp. de krachten ~F2 en ~R1. Deze werklijnen snijden elkaar in het punt P (zie figuur 2.11).
5. Ik construeer terug een parallellogram nu met als zijden ~F2 en ~R1 vanaf het punt P. De diagonaal is de resultante ~R.
1 kN F1 F2 F3 R1 F3 F1 a c O R R1 F2 P b d
Figuur 2.11: Samenstellen van krachten die elkaar niet in één punt snijden: stap 2
2.4.2 Voorbeeld 2 10 kN F1 F2 F3 F1 F2 F3 R1 R R R1 O P
Figuur 2.12: Samenstellen van krachten die elkaar niet snijden in één punt
Figuur 2.12 stelt dit probleem voor. Ik ga als volgt tewerk:
1. Ik bepaal eerst de resultante van twee krachten. Ik heb ~F1en ~F2 gekozen. Hun werklijnen snijden in punt O. Hun resultante is ~R1. Rechts heb ik de krachtendriehoek getekend.
2. De werklijn van ~R1 vertrekt vanuit O en snijdt de werklijn van de kracht ~R3 in het punt P. Door het punt P moet de werklijn van de resultante ~R doorgaan. De grootte en de zin vind ik met de krachtendriehoek (rechts in de figuur).
2.5
Ontbinden van een kracht in drie componenten waarvan de
werklijnen gegeven zijn
Om een kracht te ontbinden werk ik in de omgekeerde volgorde van het samenstellen van krachten. Er zijn twee mogelijkheden:
1. De werklijnen gaan door één punt. Dit vraagstuk is onbepaald. Men kan immers de grootte van één vector willekeurig kiezen en dan het vraagstuk oplossen.
2. De werklijnen gaan niet door één punt. Hier is slechts één oplossing mogelijk.
2.6
Samenstellen van twee krachten waarvan de werklijnen
el-kaar buiten de tekening snijden
We hebben tot nu toe de methode van de parallellogram, krachtendriehoek en de krach-tenveelhoek bestudeerd. Kenmerkend in al die gevallen was dat de werklijnen van de krachten elkaar sneden binnen het ’tekenblad’. In de praktijk komt het dikwijls voor dat de krachten elkaar snijden buiten het tekenblad. In figuur 2.13 heb ik twee dergelijke krachten getekend. De opdracht is de resultante ~R = ~F1+ ~F2 te tekenen.
10 kN
F1
F2
Figuur 2.13: Twee krachten snijden buiten het blad: opgave
Ik ga dit oplossen in vier stappen:
1. Stap 1 (zie figuur 2.14): ik bepaal de resultante ~R door middel van een krachtendriehoek. Praktisch doe je dit als volgt:
• Teken de werklijnen van de gegeven krachten.
• Teken, waar er plaats is op uw blad, twee lijnen evenwijdig met de beide werklijnen. Ze snijden in M.
• Teken de krachtendriehoek. De sluitlijn is de resultante ~R. We kennen nu de grootte, de richting en de zin van de resultante. Alleen weten we nog niet waar het ’aangrijpingspunt’ is. F1 F2 R M 10 kN F1 F2
Figuur 2.14: Twee krachten snijden buiten het blad: krachtendriehoek
2. Stap 2 (zie figuur 2.15): ik teken een poolfiguur. Ik kies een (willekeurig) punt P naast de krachtendriehoek en teken lijnen naar de begin en eindpunten van de vectoren. Vervolgens splits ik de twee krachten ~F1 en ~F2 elk in twee nieuwe krachten maar wel zodanig dat ze één kracht gemeenschappelijk hebben die tegengesteld is. In mijn figuur toon ik dat door middel van de twee krachtendriehoeken die ik uiterst rechts getekend heb. De krachten ~2 en ~20 zijn gelijk maar tegengesteld en vallen samen in de poolfiguur. Hun resultante is dus nul.
F1 F2 R 1 2 & 2' 3 F1 1 2 2' 3 F2 poolfiguur P M N 10 kN F1 F2
Praktisch doe je dit als volgt:
• Teken een (bij voorkeur horizontale) lijn NP door M die de werklijnen van de beide krachten snijdt. P ligt bij mij rechts van de werklijnen. Dit punt noemt de pool. De afstand MP is (nog) niet belangrijk.
• Teken vanuit de pool P twee werklijnen die resp. door het begin- en eindpunt van ~
F1 en ~F2 gaan.
• We kunnen nu de volgende vectoren definiëren: ~F1= ~1 + ~2 en ~F2= ~20+ ~3. Het is duidelijk dat ~F1+ ~F2 = ~R = ~1 + ~3.
3. Stap 3 (zie figuur 2.16): ik teken de stangenveelhoek.
In de stap 2 heb ik de krachten gesplitst zodat: ~F1 = ~1 + ~2 en ~F2 = ~20+ ~3. Ik ga nu de oorspronkelijke krachten vervangen door deze nieuwe krachten, maar ik draag er wel zorg voor dat ~2 en ~20 op een gemeenschappelijke werklijn NMP liggen (zo kunnen ze elkaar opheffen). Praktisch doe je dit als volgt:
• Bepaal de snijpunten van de poollijn NMP met de werklijnen van ~F1 en ~F2.
• Noem het lijnstuk afgesneden door de werklijnen II (omdat de krachten ~2 en ~20 er op liggen).
• Teken door deze snijpunten werklijnen resp. evenwijdig met ~1 en ~3.
• Benoem deze werklijnen resp. I (overeenkomstig ~1) en III (overeenkomstig ~3).
• Teken nu op deze werklijnen de krachten ~1 , ~2 , ~20 en ~3.
• Vervang nu ~F1 door ~1 en ~2. Vervang ~F2 door ~20 en ~3.
• Nu heffen ~2 en ~20 elkaar op, alleen ~1 en ~3 blijven over.
1 2 3 2' stangenveelhoek I III II O 1 2 & 2' 3 poolfiguur P F1 F2 R 10 kN F1 F2 N M
4. Stap 4 (zie figuur 2.17): de resultante ~R.
In de voorgaande stap heb ik de krachten ~F1 en ~F1 vervangen door resp. de krachten ~1 en ~3. Deze snijden elkaar in het punt O. Dit punt ligt wel binnen ons tekenblad. Hiermee heb ik ons probleem opgelost.
1 3 stangenveelhoek I III II O 1 2 & 2' 3 poolfiguur P F1 F2 R 10 kN F1 F2 R
Figuur 2.17: Twee krachten snijden buiten het blad: resultante
Praktisch doe je dit als volgt:
• Teken door het snijpunt O van stangen I en III een werklijn evenwijdig met die van de resultante ~R in de poolfiguur.
• Plaats nu een vector ~R op deze werklijn. Hiermee is ons probleem opgelost.
De techniek van poolfiguur en stangenveelhoek zullen we nog dikwijls gebruiken.
2.7
Elementen van poolfiguur en stangenveelhoek
In de paragraaf 2.6 heb je kennis gemaakt met de poolfiguur en stangenveelhoek. Ik som hier een aantal bouwstenen op:
• Pool: het door ons gekozen punt van waaruit de poolstralen vertrekken.
• Poolstraal: de verbindingslijn van pool tot begin- en/of eindpunt van een krachtvector.
• Verdeelstraal: de straal die een krachtvector verdeelt.
• Verdeelpunt: het punt waar vector en verdeelstraal elkaar snijden.
• Stang: een lijn evenwijdig met een verdeelstraal die de werklijnen van twee krachten snijdt.
2.8
Samenstellen van meerdere krachten waarvan de werklijnen
elkaar buiten de tekening snijden
In de vorige paragraaf 2.6 waren er maar twee krachten. Maar wat als er meerdere krachten zijn? Wel, de werkwijze is juist dezelfde als beschreven in 2.6. Ik leg het uit aan de hand van een voorbeeld met vier krachten. Voor de opgave zie figuur 2.18.
10 kN
F1
F4 F2
F3
Figuur 2.18: Meerdere krachten snijden buiten het blad: opgave
1. Stap 1 (zie figuur 2.19): ik teken de werklijnen van de krachten en ’ergens’ op mijn blad teken ik de krachtenveelhoek. De resultante is ~R.
F1 F2 F3 F4 R 10 kN F1 F4 F2 F3
Figuur 2.19: Meerdere krachten snijden buiten het blad: krachtenveelhoek
2. Stap 2 (zie figuur 2.20 ): ik teken de poolfiguur. De pool is P en de vectoren zijn ~1 tot en met ~5.
F1 F2 F3 F4 R 1 2 3 4 5 P 10 kN F1 F4 F2 F3
Figuur 2.20: Meerdere krachten snijden buiten het blad: poolfiguur
3. Stap 3 (zie figuur 2.21 ): ik teken de stangenveelhoek. Herinner dat op de werklijn van kracht ~F1 de stangen I en II elkaar snijden, enz... Het snijpunt van de stangen I en V is O. Het is het punt waar de werklijn van de resultante zal doorgaan.
F1 F2 F3 F4 R 1 2 3 4 5 P 10 kN F1 F4 F2 F3 I II III IV V O
Figuur 2.21: Meerdere krachten snijden buiten het blad: stangenveelhoek
F1 F2 F3 F4 R 1 2 3 4 5 P R 10 kN F1 F4 F2 F3 I II III IV V O
Figuur 2.22: Meerdere krachten snijden buiten het blad: resultante
2.9
Bepalen van de resultante van evenwijdige krachten
Evenwijdige krachten zij een bijzondere vorm van krachten die elkaar snijden buiten het tekenblad (zij snijden elkaar niet). De werkwijze is volledig beschreven in paragraaf 2.8. Ik ga de werkwijze daarom alleen maar uitleggen aan de hand van onderstaande tekeningen.
Voor de opgave zie figuur 2.23.
1 kN
F1
F2
F3
F4
Figuur 2.23: Evenwijdige krachten: opgave
Noteer dat ik in de figuur 2.24 de krachten ~F4 en ~R naast hun werklijn heb getekend voor de duidelijkheid.
F1 F2 F3 F4 R 1 kN F1 F2 F3 F4
Figuur 2.24: Evenwijdige krachten: krachtenveelhoek
Figuur 2.25 : de poolfiguur. F1 F2 F3 F4 R 1 2 3 4 5 P 1 kN F1 F2 F3 F4
Figuur 2.25: Evenwijdige krachten: poolfiguur
F1 F2 F3 F4 R 1 2 3 4 5 P 1 kN F1 F2 F3 F4 I II III IV V
Figuur 2.26: Evenwijdige krachten: stangenveelhoek
Figuur 2.27 : de resultante ~R . F1 F2 F3 F4 R 1 2 3 4 5 P R 1 kN F1 F2 F3 F4 I II III IV V
Hoofdstuk 3
Evenwicht van krachten
3.1
Balk ondersteund in twee punten
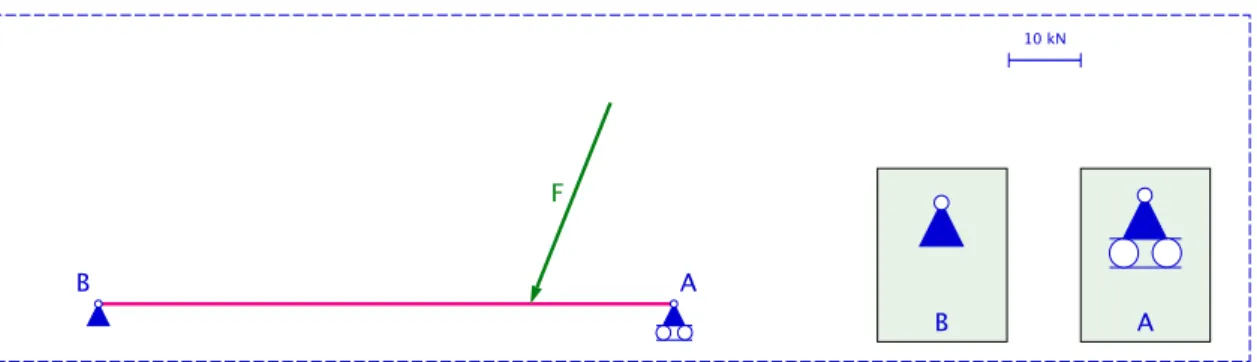
In de praktijk komen we zeer veel vaste constructies tegen die onderhevig zijn aan meerdere krachten. Bij deze constructies moeten alle krachten in evenwicht zijn. Nemen we als voorbeeld een balk die ondersteund wordt in de beide uiteinden en waarop één kracht, in ons geval een puntlast, inwerkt (zie figuur 3.1).
10 kN
B A
F
B A
Figuur 3.1: Balk ondersteund in uiteinden en belast met puntlast: opgave
Op het eerste zicht ’werkt’ er maar één kracht ~F op de balk. Maar omdat de balk niet beweegt moeten er nog andere krachten zijn die evenwicht maken met ~F . Deze ’onzichtbare’ krachten treden op in de steunpunten. Het zijn de steunpunt reactiekrachten. Ik noem ze ~Ra en ~Rb. Er is evenwicht als ~F = ~Ra+ ~Rb. Dit komt erop neer dat de krachtenveelhoek gesloten is.
Ik moet eerst iets vertellen over de steunpunten A en B. Rechts in de figuur heb ik ze vergroot getekend. Het steunpunt A noemen we een roloplegging. Het steunpunt B noemen we een scharnieroplegging. Bij een roloplegging staat de werklijn van de reactiekracht steeds loodrecht op het steunvlak. Bij een scharnieroplegging kan de werklijn van de reactiekracht alle richtingen aannemen.
Om nu de reactiekrachten ~Ra en ~Rb te kunnen bepalen moet ik de kracht ~F ontbinden in twee componenten waarvan de richting van de werklijn van ~Ragekend is (die laatste staat loodrecht op het steunvlak omdat er in A een roloplegging is).
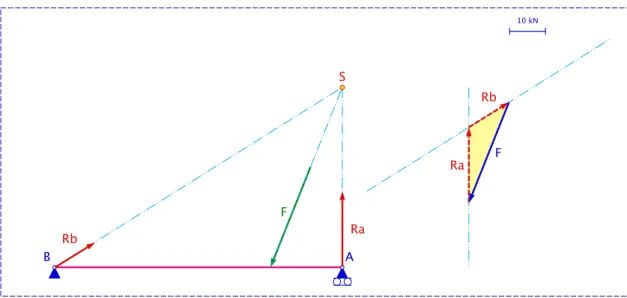
Ik ga als volgt tewerk (zie figuur 3.2):
1. Ik teken de werklijn van ~F en ~Ra.
2. Het snijpunt van de beide werklijnen noem ik S.
3. Ik teken de lijn BS. Dit is de werklijn van van ~Rb. Ik beschik nu over alle werklijnen.
4. Ik construeer nu een krachtenveelhoek (zie rechts op de tekening). Ik teken eerst de kracht ~F . Door het beginpunt van ~F teken ik een lijn evenwijdig met de werklijn van
~
Rb. Door het eindpunt van ~F teken ik een lijn evenwijdig met de werklijn van ~Ra.
5. De zin van de ~Ra en ~Rb kies ik zo dat de krachtenveelhoek gesloten is.
6. Tenslotte breng ik de krachten ~Ra en ~Rb over naar hun aangrijpingspunten A en B.
10 kN B A F F Ra Rb Ra Rb S
Figuur 3.2: Balk ondersteund in uiteinden en belast met puntlast: oplossing
3.2
Spant
Een spant is een constructie die wanden en/of een dak draagt zoals afgebeeld in figuur 3.3. In ons voorbeeld is het spant blootgesteld aan drie uitwendige krachten. De krachten en het spant zijn op schaal getekend. Ons spant steunt in A op een scharnieroplegging en in B op een roloplegging. Gevraagd wordt de reactiekrachten in de steunpunten te bepalen. Noteer dat ik in dit voorbeeld geen rekening houd met het eigengewicht van de constructie.
1 kN 1 m A B F1 F2 F3 D C
Figuur 3.3: Spant: opgave
Los dit probleem als volgt op:
1. Bepaal de resultante ~R van de drie uitwendige krachten ~F1, ~F2 en ~F3. Zie figuur 3.4.
• Teken de werklijnen van de krachten ~F1 en ~F2 tot ze elkaar snijden in M.
• Teken de krachtendriehoek op ~F1 en ~F2. De resultante is ~R1.
1 kN 1 m A B F1 F2 F3 D C M N F1 F2 R1 F3 R1 R
• Teken de werklijnen van de krachten ~F3 en ~R1 tot ze elkaar snijden in N.
• Teken de krachtendriehoek op ~F3 en ~R1. De resultante is ~R.
• De resultante van de uitwendige krachten is: ~R = ~F1+ ~F2+ ~F3.
2. Splits de resultante ~R in de reactiekrachten ~Raen ~Rb. Zie figuur 3.5.
• Teken de werklijn van ~R en de werklijn van de reactiekracht ~Rb. Ze snijden elkaar in P. Noteer dat de werklijn in B loodrecht op het steunvlak van de roloplegging staat.
• Teken de lijn AP, dit is de werklijn van ~Ra.
• Splits ~R in ~Ra en ~Rb zodat ~Rb+ ~Ra= ~R door middel van een krachtendriehoek.
• Verschuif ~Ra en ~Rb naar hun aangrijpingspunten.
1 kN 1 m A B F1 F2 F3 D C R Rb Ra Rb Ra R P
Figuur 3.5: Spant: de reactiekrachten in de steunpunten
3.3
Driescharnierspant
Een driescharnierspant is een spantenconstructie die uit twee helften bestaat. De twee helften zijn door middel van een scharnier met elkaar verbonden. De krachten die de beide helften op elkaar uitoefenen kunnen alle richtingen uit.
3.3.1 Driescharnierspant voorbeeld 1
Figuur 3.6 stelt een driescharnierspant voor waarop één uitwendige kracht op het linkerdeel inwerkt. Via het scharnier C oefenen de beide helften gelijke maar tegengestelde krachten op elkaar uit. De steunpuntkrachten, de uitwendige en de inwendige krachten vormen samen een gesloten krachtenveelhoek (dus de resultante is nul). Bijgevolg moet elk deel op zich in evenwicht zijn. We mogen daarom elk deel afzonderlijk behandelen. Ik los dit probleem op in drie stappen.
10 kN
A B
C
F
Figuur 3.6: Driescharnierspant 1: opgave
1. Stap 1: zie figuur 3.7. Aangezien er op de rechtse span geen uitwendige krachten inwerken moet de steunpuntkracht ~Rb en de scharnierkracht ~Rcgelijk en tegengesteld zijn en op dezelfde werklijn liggen. Deze werklijn is BC. Het linkse spant is in evenwicht onder invloed van de steunpuntkracht ~Ra, de uitwendige kracht ~F en scharnierkracht ~Rc. Dit gezegd zijnde kunnen we aan de oplossing beginnen.
F Rc Ra A B C F M 10 kN
• Ik teken de werklijnen van de kracht ~F en ~Rc (ligt op BC). Ze snijden elkaar in het punt M.
• Ik veronderstel dat het rechtse spant er niet is (daarom heb ik het in stippellijn getekend).
• Ik verschuif de kracht ~F langs zijn werklijn totdat haar beginpunt samenvalt met M.
• Ik teken de werklijn AM (hierop komt de steunpuntkracht ~Ra op te liggen).
• Ik teken een werklijn door het eindpunt van de kracht ~F parallel met BC.
• Ik heb op die manier een (gesloten) krachtendriehoek gevormd. ~Ra en ~Rczijn nu bepaald. Ra Rc Rc A B C F Ra F Rc 10 kN
Figuur 3.8: Driescharnierspant 1: stap 2
Rb A B F C Rc' Ra Rc 10 kN
2. Stap 2: zie figuur 3.8. Ik heb hier de linkse spant getekend met alle krachten die het in evenwicht houdt.
3. Stap 3: zie figuur 3.9. Nu bekijk ik alleen de rechtse spant. De scharnierkracht ~Rc0 is gelijk maar tegengesteld aan ~Rc (die heb ik bepaald in stap 2). ~Rb moet evenwicht maken met ~Rc0. Dit geeft ons de getekende oplossing. Daarmee zijn ~Ra en ~Rb bepaald.
3.3.2 Driescharnierspant voorbeeld 2
Zie figuur 3.10. In dit voorbeeld werken er op elke spant een uitwendige kracht.
1 kN 1 m A C Rl Rr B
Figuur 3.10: Driescharnierspant 2: opgave
Rl Ral Ral A Rl B Rcl C O Rcl Rcl Rcl' 1 kN 1 m
Figuur 3.11: Driescharnierspant 2: stap 1
Ik los dit zoals beschreven in paragraaf 3.3.1 voor het linkse en rechtse spant afzonderlijk. Daarna superponeer ik de beide resultaten.
1. In stap 1 (zie figuur 3.11) doe ik alsof er geen kracht op het rechtse deel staat. Het linkse deel ondervindt wel een reactiekracht van het rechtse deel.
• Teken de werklijn van ~Rl en de werklijn van ~Rcl (is CB). Het snijpunt van beide werklijnen is O.
• Teken de werklijn AO.
• Verschuif ~Rl totdat de oorsprong samenvalt met O.
• Teken een werklijn evenwijdig met AO die door het eindpunt van de kracht ~Rl gaat.
• We hebben nu een driehoek met als zijden ~Rl, ~Ral en ~Rcl.
• Verschuif nu ~Ral naar A en ~Rcl naar C.
2. In stap 2 (zie figuur 3.12) doe ik alsof er geen kracht op het linkse deel staat. Het rechtse deel ondervindt wel een reactiekracht van het linkse.
Rbr Rr Rr A C Rcr B P Rcr Rbr Rcr' Rcr 1 kN 1 m
Figuur 3.12: Driescharnierspant 2: stap 2
• Teken de werklijn van ~Rr en de werklijn van ~Rcr (is AC). Het snijpunt van beide werklijnen is P.
• Teken de werklijn BP.
• Verschuif ~Rr totdat de oorsprong samenvalt met P.
• Teken een werklijn evenwijdig met AC die door het eindpunt van de kracht ~Rr gaat.
• We hebben nu een driehoek met als zijden ~Rr, ~Rcr en ~Rbr.
• Teken de krachten die inwerken op steunpunt B en maak som: dit geeft ~Rb.
• Teken de krachten die inwerken op scharnierpunt C en maak som: dit geeft ~Rcen ~ Rc0. 1 kN 1 m A C Rl Rr B Ral Rbr Ra Rb Rc Rc' Rcr Rcl Rcr Rcr' Rcl' Rcl
Figuur 3.13: Driescharnierspant 2: stap 3
3.4
Vakwerk
Een vakwerk is een spant bestaande uit liggers en stangen. In dit voorbeeld (zie figuur 3.14) wordt het spant belast met vier puntlasten. Gevraagd wordt de resultante van deze vier krachten te bepalen. Ik los dit op met de techniek die ik in paragraaf 2.8 beschreven heb.
10 kN
F1
F2
F3
F4
Figuur 3.14: Vakwerk 1: opgave
Ik voer de volgende stappen uit:
1. Ik teken een krachtenveelhoek en bepaal de grootte, richting en zin van de resultante ~R.
3. Ik teken de werklijnen door de krachten en de stangenveelhoek. De resultante gaat door het snijpunt O. F1 F2 F3 F4 R 10 kN F1 F2 F3 F4
Figuur 3.15: Vakwerk 1: krachtenveelhoek
F1 F2 F3 F4 R 1 2 3 4 5 P 10 kN F1 F2 F3 F4
Figuur 3.16: Vakwerk 1: poolfiguur
F1 F2 F3 F4 R 1 2 3 4 5 P 10 kN F1 F2 F3 F4 I II III IV V O R
3.5
Steunpunt reactiekrachten van belaste liggers
Ik behandel dit onderwerp aan de hand van een aantal voorbeelden. In paragraaf 3.1 heb ik de eigenschappen van de steunpunten behandeld. In de paragraaf 2.6 en 2.8 heb ik de poolfiguur en stangenveelhoek in detail behandeld. We hebben de kennis hiervan nodig om de volgende problemen op te lossen.
Belangrijke opmerking: in de tekeningen die volgen teken ik de krachten soms juist naast elkaar. Ik doe dit enkel ten behoeve van de duidelijkheid, in werkelijkheid liggen deze krachten op elkaar.
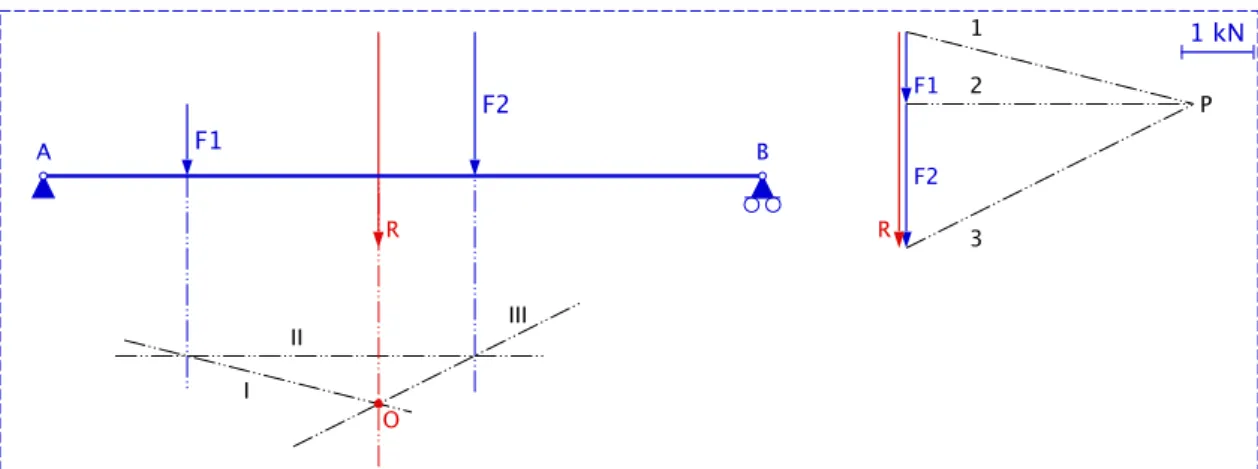
3.5.1 Voorbeeld 1: ligger belast met puntlasten
1 kN
F1
F2
A B
Figuur 3.18: Ligger belast met puntlasten: opgave
Ik los dit op in vijf stappen:
1. Stap 1: zie figuur 3.19 . Teken de poolfiguur.
• Opmerking 1: ik heb de resultante ~R voor duidelijkheid naast de krachten ~F1 en ~
F2 getekend (ik zal dit in de volgende figuren ook doen).
• Opmerking 2: de poollijn van ~2 neem ik voor het gemak horizontaal.
F1 F2 R 1 2 3 P 1 kN F1 F2 A B
Figuur 3.19: Ligger belast met puntlasten: poolfiguur
F1 F2 R 1 2 3 P I II III R O 1 kN F1 F2 A B
Figuur 3.20: Ligger belast met puntlasten: stangenveelhoek en resultante
3. Stap 3: zie figuur 3.21. Nu moeten we de resultante ~R splitsen in de reactiekrachten ~Ra en ~Rb. We zullen nu de techniek van poolfiguur en stangenveelhoek omgekeerd gebruiken.
• Teken de werklijnen van de reactiekrachten.
• Teken een nieuw poolfiguur met ~R als enige kracht en kies een pool. Ik heb Q gekozen. De poolafstand van beide poolfiguren moet dezelfde zijn.
• Teken de vectoren ~5 en ~6.
• Teken de poollijnen V en VI.
• Teken de sluitlijn VII en teken een werklijn (7) door Q evenwijdig met VII.
F1 F2 R 1 2 3 P I II III R O 1 kN F1 F2 A B 5 6 R 7 VII V VI Q
4. Stap 4: zie figuur 3.22. De ~7 deelt ~R in twee vectoren: ~Ra en ~Rb. ~Ra ligt tussen ~5 (op het snijpunt van stangen V en VII) en ~7 (op het snijpunt van stangen VI en VII).
F1 F2 R 1 2 3 P I II III R O Rb Ra Rb Ra 1 kN F1 F2 A B VII V VI 5 6 R 7 Q
Figuur 3.22: Ligger belast met puntlasten: poolfiguur en reactiekrachten
5. Stap 5: zie figuur 3.23. Teken de twee reactiekrachten: ~Ra en ~Rb.
F1 F2 R 1 2 3 P I II III R O Rb Ra Rb Ra 1 kN F1 F2 A B VII V VI 5 6 R 7 Q Ra Rb
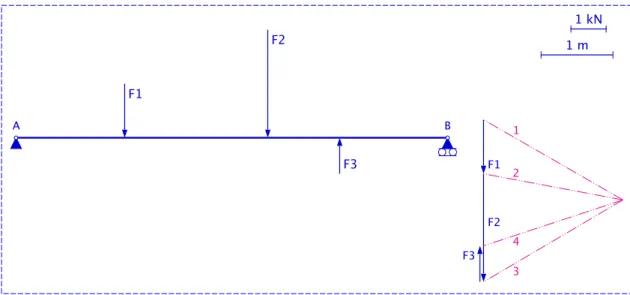
3.5.2 Voorbeeld 2: ligger belast met puntlasten
Opgave zie figuur 3.24. In dit tweede voorbeeld is de balk ondersteund in de eindpunten en werken er drie puntlasten loodrecht op de balk. De oplossing verloopt analoog met voorbeeld 1 maar ik ga een aantal stappen samenvoegen.
1 kN F1 A B 1 m F2 F3
Figuur 3.24: Ligger belast met puntlasten: opgave
1. Stap 1. Figuur 3.25 . Ik teken de poolfiguur. Let op de zin van de kracht ~F3 (is naar boven gericht).
2. Stap 2. Figuur 3.26 . Ik teken de stangenveelhoek en bepaal de snijpunten van de stangen I en IV met de werklijnen van de reactiekrachten.
3. Stap 3. Figuur 3.27 . Ik teken de sluitlijn van de stangenveelhoek: stang V. Door het poolpunt P teken ik een werklijn evenwijdig met stang V. De reactiekrachten zijn nu ook bepaald. ~Ra ligt tussen ~5 en ~1. ~Rb ligt tussen ~4 en ~5. Ik breng de reactiekrachten
~
Ra en ~Rb over naar hun werklijnen.
1 2 3 4 F1 F2 F3 1 kN F1 A B 1 m F2 F3
1 2 3 4 F1 F2 F3 I II III IV 1 kN F1 A B 1 m F2 F3
Figuur 3.26: Ligger belast met puntlasten: stangenveelhoek
1 2 3 4 F1 F2 F3 I II III IV P 1 kN F1 A B 1 m F2 F3 5 Rb Ra Rb Ra V Ra Rb
3.5.3 Voorbeeld 3: ligger belast met puntlasten en gelijkmatige lasten
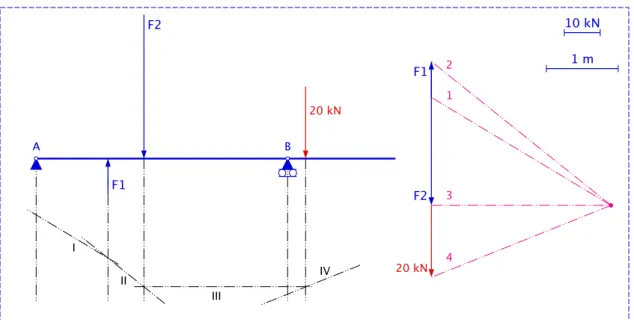
Opgave zie figuur 3.28. In dit voorbeeld is de balk maar ondersteund in één uiteinde. Er is dus een overhangend deel. Bovendien is er een gelijkmatige belasting. In het voorbeeld bedraagt de gelijkmatige last 8 kN/m de lengte ervan is 2,5 m.
10 kN F1 F2 A B 1 m 8 kN/m
Figuur 3.28: Ligger belast met puntlasten en gelijkmatige last: opgave
1. Stap 1. Figuur 3.29. Ik heb de gelijkmatige last omgerekend naar een puntlast en laat die aangrijpen in het zwaartepunt ervan. De puntlast bedraagt 20 kN. Ik teken de poolfiguur.
2. Stap 2. Figuur 3.30. Ik teken de stangenveelhoek en de werklijnen van de reactiekrachten.
3. Stap 3. Figuur 3.31 . Ik teken de sluitlijn van de stangenveelhoek: stang V. Door het poolpunt P teken ik een werklijn evenwijdig met stang V. De reactiekrachten zijn nu ook bepaald. ~Ra ligt tussen ~5 en ~1. ~Rb ligt tussen ~4 en ~5. Ik breng de reactiekrachten
~
Ra en ~Rb over naar hun werklijnen.
1 2 3 4 F1 F2 20 kN 10 kN F1 F2 A B 1 m 20 kN
1 2 3 4 F1 F2 20 kN I II III IV 10 kN F1 F2 A B 1 m 20 kN
Figuur 3.30: Ligger belast met puntlasten en gelijkmatige last: stangenveelhoek
1 2 3 4 F1 F2 20 kN I II III IV 5 V Rb Ra Rb Ra P 10 kN F1 F2 A B 1 m 8 kN/m 20 kN
Figuur 3.31: Ligger belast met puntlasten en gelijkmatige last: reactiekrachten
3.5.4 Voorbeeld 4: ligger belast met schuine puntlasten
Opgave zie figuur 3.32 . In dit voorbeeld is de balk maar ondersteund in één uiteinde, er is een overhang. Het steunpunt A is een roloplegging. De werklijn van de steunpuntreactie in A moet dus loodrecht op de balk staan. De reactiekracht in de scharnieroplegging in B zal dus schuin staan. Deze opgave ga ik terug in drie stappen oplossen.
10 kN F1 A B 1 m F5 F4 F2 F3
Figuur 3.32: Ligger belast met schuine puntlasten: opgave
1. Stap 1. Zie figuur 3.33. Ik teken de poolfiguur en bepaal de resultante ~R van de puntlasten. F4 F1 F5 F2 F3 1 2 3 4 6 5 R P 10 kN F1 A B 1 m F5 F4 F2 F3
Figuur 3.33: Ligger belast met schuine puntlasten: poolfiguur
2. Stap 2. Zie figuur 3.34. Ik teken de stangenveelhoek. De resultante ~R ligt op het snijpunt van de stangen I en VI.
F4 F1 F5 F2 F3 1 2 3 4 6 5 R P I II III IV VI V R b 10 kN F1 A B 1 m F5 F4 F2 F3
Figuur 3.34: Ligger belast met schuine puntlasten: stangenveelhoek
3. Stap 3. Zie figuur 3.35. Nu moet ik ~R ontbinden in ~Ra en ~Rb. De werklijn van ~Rais de lijn a en staat loodrecht op de balk. De werklijn van ~R noem ik b. De werklijnen a en b snijden elkaar in S. De werklijn van ~Rb moet door B en door S gaan. Ik noem deze werklijn c. Ik breng de lijnen a en c over naar de poolfiguur. Het snijpunt T van a en c bepaalt de reactiekrachten ~Ra en ~Rb.
F4 F1 F5 F2 F3 1 2 3 4 6 5 R P I II III IV VI V R b VII Ra Rb a c a c 7 M N Rb Ra O Q 10 kN F1 A B 1 m F5 F4 F2 F3 S T
Hoofdstuk 4
Zwaartepunt van een vlakke figuur
Het zwaartepunt van een lichaam is het punt waar we de volledige massa of gewicht mogen laten aangrijpen. Gewicht is een kracht. Een vlakke figuur heeft geen massa of gewicht maar wel een zwaartepunt.
Van een eenvoudige (symmetrische) vlakke figuur zoals een rechthoek weet je dat het zwaarte-punt aangrijpt in het snijzwaarte-punt van de diagonalen. Bij een cirkel is het het middelzwaarte-punt van de cirkel.
Ik leg de werkwijze uit aan de hand van figuur 4.1. Om het zwaartepunt van een complexe figuur te vinden ga ik de figuur opsplitsen in symmetrische figuren waarvan ik weet waar het zwaartepunt ligt. De oppervlakte van deze figuren stel ik voor door middel van een kracht die aangrijpt in het zwaartepunt.
5 cm2
Bij een vlakke figuren bestaan de coördinaten van het zwaartepunt uit twee componenten. Ik zal dus in twee verschillende richtingen moeten werken.
1. Stap 1. Zie figuur 4.2. Ik kies een schaal die het verband tussen oppervlak en kracht voorstelt. Ik deel de vlakke figuur op in drie rechthoeken. Ik teken de diagonalen en bereken de oppervlakte van deze rechthoeken. Rekening houdend met de schaal laat ik in het zwaartepunt van elke rechthoek twee krachten aangrijpen. De ene kracht gaat horizontaal naar rechts en de andere gaat verticaal naar beneden. Deze krachten zijn het ’gewicht’ van elke rechthoek.
5 cm2 F1 F2 F3 F3 F2 F1
Figuur 4.2: Zwaartepunt van een vlakke figuur: stap 1
2. Stap 2. Zie figuur 4.3. Ik bepaal de resultante van de resp. de horizontale en verticale krachten. Dit zijn ~Rhen ~Rv. Het snijpunt van de werklijnen van ~Rh en ~Rv is het gezochte zwaartepunt.
5 cm2 Z 1 2 3 4 1 2 3 4 I II III IV I II III IV Rh Rv F1 F2 F3 F3 F2 F1 F1 F2 F3 F3 F2 F1
Hoofdstuk 5
Momenten- en dwarskrachtenlijn
5.1
Inleiding
In een balk die belast wordt treden er dwarskrachten en buigende momenten op. Deze zijn bepalend voor het materiaal en doorsnede van de balk. In de sterkteleer berekenen we deze krachten. In de grafostatica zullen we ze grafisch bepalen. In mijn tekeningen zullen dus meerdere schalen voorkomen:
• Krachtenschaal. Krachtenschaal is ons reeds bekend: x [cm] ≡ y [kN].
• Lengteschaal. Lengteschaal is ons ook reeds bekend: x [cm] ≡ y [m].
• Poolafstand. Poolafstand hebben we gebruikt bij de poolfiguren: x [cm] ≡ y [m].
• Momentenschaal. Momentenschaal is nieuw: x [cm] ≡ y [kNm].
5.2
Het moment van een evenwijdige krachten ten opzichte van
een punt
Zie figuur 5.1. Ik heb een stel van vier evenwijdige krachten en een punt Q. Ik wens het moment van deze krachten ten opzichte van het punt Q te kennen.
Om dit op te lossen teken ik een poolfiguur (de poolafstand is h), de stangenveelhoek en een lijn evenwijdig met de krachten door het punt Q. Deze lijn noemen we de leeslijn. In de figuur heb ik twee driehoeken gekleurd. Ze zijn gelijkvormig omdat hun zijden evenwijdig zijn, bijgevolg is:
EG
F =
a h
F1 F2 F3 F4 1 2 3 4 5 P h I II III IV V Q E N a G 1 kN F1 F2 F3 F4 1 m
Figuur 5.1: Het moment van evenwijdige krachten ten opzichte van een punt
Met moment M van ~F1 ten opzichte van de leeslijn is:
M = F1a = EG · h
In woorden uitgedrukt: het moment van een kracht ten opzichte van een leeslijn is gelijk aan het product van de lengte van het lijnstuk dat afgesneden wordt door de stangen die samenkomen op de werklijn van de kracht en de poolafstand.
Indien ik deze stelling toepas voor alle krachten van de figuur dan is het moment ten opzichte van het punt Q:
ΣM = EN · h
Opgelet:
• Bij de lengte van de lijnstukken op de leeslijn dien je rekening te houden met de lengtenschaal.
5.3
In de einden ondersteunde balk met puntlasten
Opgave zie figuur 5.2. De balk wordt ondersteund in de eindpunten en wordt belast met drie verticale puntlasten. Opdracht: teken de momenten- en dwarskrachtenlijn.
1 m 1 kN
F1
F2
F3
Figuur 5.2: In de einden ondersteunde balk met puntlasten: opgave
Deze opdracht ga ik in drie stappen oplossen.
1. Stap 1. Zie figuur 5.3. Ik bepaal de reactiekrachten in de steunpunten. Herinner dat a · h het moment is ter hoogte van de werklijn van ~F1 (zie paragraaf 5.2). Daar h vast ligt is a een maat voor het moment.
1 m 1 kN F1 F2 F3 1 2 3 4 I II III IV V Ra Rb Ra Rb 5 h a
Figuur 5.3: In de einden ondersteunde balk met puntlasten: stap 1
2. Stap 2. Zie figuur 5.4. Ik herteken de stangenveelhoek en draag er zorg voor dat de sluitlijn V horizontaal is. De nieuwe veelhoek stelt het buigend moment voor. Let op
1 m 1 kN F1 F2 F3 1 2 3 4 I II III IV V Ra Rb Ra Rb 5 BUIGEND MOMENT poolafstand 4 kNm 8,2 kNm 6,8 kNm 5 kNm lengteschaal: 1 cm <> 0,5 m krachtenschaal: 1 cm <> 2 kN poolafstand 4 cm <> 8 kN (4 * 2 = 8) momentschaal: 1 cm <> 8kN * 0,5 m = 4 kNm
Figuur 5.4: In de einden ondersteunde balk met puntlasten: stap 2
1 m 1 kN F1 F2 F3 F1 F2 F3 Ra Rb DWARSKRACHTEN A B Ra Rb lengteschaal: 1 cm <> 0,5 m krachtenschaal: 1 cm <> 2 kN poolafstand 4 cm <> 8 kN (4 * 2 = 8) momentschaal: 1 cm <> 8kN * 0,5 m = 4 kNm
Figuur 5.5: In de einden ondersteunde balk met puntlasten: stap 3
• Teken een horizontale lijn.
• In A is de dwarskracht Ra.
• Ter hoogte van de werklijn van ~F1 neemt de dwarskracht met de grootte F1 af. Dit gaat zo verder tot ik met Rb terug op de nullijn in B kom.
5.4
In twee punten ondersteunde balk met overstekende einden
en puntlasten
Opgave zie figuur 5.6. De balk wordt ondersteund in twee punten, is aan beide zijden overstekend en wordt belast met vier verticale puntlasten.
1 m 10 kN F1 F2 F3 F4 A B
Figuur 5.6: In twee punten ondersteunde balk met overstekende einden en puntlasten: opgave
Deze opdracht ga ik in drie stappen oplossen. De oplossing verloopt volledig analoog met de vorige paragraaf. 1 m 10 kN F1 F2 F3 F4 A B 1 2 3 4 I II III V VI Ra Rb Ra Rb 5 IV 6
1. Stap 1. Zie figuur 5.7. Ik bepaal de reactiekrachten in de steunpunten. De lijnstukken die door de stangen ter hoogte van de werklijnen worden gesneden zijn een maat voor het moment.
2. Stap 2. Zie figuur 5.8. Ik herteken de stangenveelhoek en draag er zorg voor dat de sluitlijn V horizontaal is. De nieuwe veelhoek stelt het buigend moment voor. Let op de schalen. 1 m 10 kN F1 F2 F3 F4 A B 1 2 3 4 I II III V VI Ra Rb Ra Rb 5 IV 6 lengteschaal: 1 cm <> 0,5 m krachtenschaal: 1 cm <> 5 kN poolafstand 4 cm <> 4 * 5 = 20 kN momentschaal: 1 cm <> 20 kN * 0,5 m = 10 kNm
BUIGEND MOMENT poolafstand
10 kNm 8 kNm
6 kNm
6 kNm 4 kNm
Figuur 5.8: In twee punten ondersteunde balk met overstekende einden en puntlasten: stap 2
3. Stap 3. Zie figuur 5.9 . De dwarskrachtenlijn is eenvoudig te construeren:
• Teken een horizontale lijn.
• Ter hoogte van de werklijn van ~F1 heeft de dwarskracht de grootte F1. Ik teken de dwarskracht steeds tegengesteld aan de pijl van de vector (dus als de vectorpijl naar beneden wijst dan teken ik de dwarskracht omhoog).
• In A wijzigt de dwarskracht met de grootte Ra ( ~Rawijst omhoog, ik teken daarom de dwarskracht naar beneden).
1 m 10 kN F1 F2 F3 F4 A B F1 F2 F3 Ra Rb DWARSKRACHTEN F4 Ra Rb lengteschaal: 1 cm <> 0,5 m krachtenschaal: 1 cm <> 5 kN poolafstand 4 cm <> 4 * 5 = 20 kN momentschaal: 1 cm <> 20 kN * 0,5 m = 10 kNm
Figuur 5.9: In twee punten ondersteunde balk met overstekende einden en puntlasten: stap 3
5.5
In de einden ondersteunde balk met puntlasten en
gelijkma-tige belasting
Opgave zie figuur 5.10. De balk wordt ondersteund in de einden en wordt belast met twee verticale puntlasten en een gelijkmatige last. Opdracht: teken de momenten- en dwarskrach-tenlijn. 1 m 1 kN F1 F2 0,4 kN/m A B
vorige paragraaf.
1. Stap 1. Zie figuur 5.11 . Ik vervang eerst de gelijkmatige last door een puntlast ~Q die aangrijpt in haar zwaartepunt. Ik heb nu drie puntlasten en een balk ondersteund in de einden. Vanaf nu verloopt de oplossing zoals beschreven in paragraaf 5.3. Noteer dat de buigend momentenlijn hier het verloop van puntlasten weergeeft. Onder de gelijkmatige last is het een kromme. Maar dit speelt hier geen rol omdat we op zoek zijn naar de maximum waarde.
1 m 1 kN F1 F2 0,4 kN/m A B 1 2 3 4 I II III V Ra Rb Ra Rb IV 5 Q Q F1 F2 BUIGEND MOMENT poolafstand lengteschaal: 1 cm <> 0,5 m krachtenschaal: 1 cm <> 0,5 kN poolafstand 4 cm <> 4 * 0,5 = 2 kN momentschaal: 1 cm <> 2 kN * 0,5 m = 1 kNm 10 kNm
Figuur 5.11: In de einden ondersteunde balk met puntlasten en gelijkmatige belasting: stap 1
2. Stap 2. Zie figuur 5.12. Nu teken ik de dwarskrachtenlijn alsof het allemaal puntlasten zijn die de balk belasten. Indien de kracht ~F2 er niet was dan zou de dwarskracht volgens de rechte MN verlopen. Maar door de kracht ~F2 wordt deze rechte gebroken. Het snijpunt O van MN met de horizontale as is het punt waar het buigend moment maximaal is. De benaderende waarde ervan kunnen aflezen onder de buigend momentenlijn.
1 m 1 kN F1 F2 0,4 kN/m A B F1 F2 Ra Rb DWARSKRACHTEN Q lijn v an m axim aal bu ig en d m om en t F2 M N O Ra Rb
Figuur 5.12: In de einden ondersteunde balk met puntlasten en gelijkmatige belasting: stap 2
5.6
Balk met enkel een gelijkmatige belasting
Opgave zie figuur 5.13. De balk wordt niet in de einden ondersteund en heeft over de volledige lengte een gelijkmatige belasting. Opdracht: teken de momenten- en dwarskrachtenlijn.
1 m 0,2 kN 0,2 kN/m
A B
Figuur 5.13: Balk met gelijkmatige belasting: opgave
1 m 0,2 kN 0,2 kN/m A B 1 2 I III Ra Rb Ra Rb 3 1,44 kN II 0,54 kN 0,9 kN
Figuur 5.14: Balk met gelijkmatige belasting: reactiekrachten
2. Stap 2. De dwarskrachten: zie figuur 5.15. Ik deel de gelijkmatige last op in drie delen: een deel links van A, een deel tussen A en B en een deel rechts van B. Ik bereken hun grootte. Ik kan nu de dwarskrachtenlijn tekenen. Het zijn lijnen die recht verlopen tussen de uiterste punten. In het punt M is de dwarskracht nul en zal het buigend moment maximaal zijn. 1 m 0,2 kN 0,2 kN/m A B Ra Rb DWARSKRACHTEN 0,12 kN 0,96 kN 0,36 kN 0,12 0,36 Ra Rb M
Figuur 5.15: Balk met gelijkmatige belasting: dwarskrachten
3. Stap 3. Het buigend moment: zie figuur 5.16. Bij gelijkmatige belasting is het buigend moment een kromme. Het maximum treedt op waar de dwarskracht nul is.
1 m 0,2 kN 0,2 kN/m Ra Rb 0,12 kN 0,96 kN 0,36 kN BUIGEND MOMENT 0,1 kNm C A B D M max
Hoofdstuk 6
Vakwerken
6.1
Inleiding
Een vakwerk is een technische constructie die uit rechte staven is opgebouwd. De staven zijn met elkaar verbonden en vormen drie- of veelhoeken. Het punt waar de staven samenkomen noemt men knooppunt. Bij de berekening gaan we ervan uit dat de staven in de knooppunten scharnierend met elkaar verbonden zijn. Hierdoor kunnen er alleen maar zuivere trek- of drukkrachten in de staven optreden. Verder wordt het eigengewicht van de staaf als een belasting gezien die in de knooppunten aangrijpt.
Men onderscheidt platte en ruimte vakwerken. Ik beperk mij tot de platte vakwerken. Belangrijk is ook dat er niet meer staven dan noodzakelijk zijn gebruikt (de zogenaamde inwendig statisch bepaalde vakwerken).
Ik zal spanten, luifels, kolommen, bruggen en kranen gebruiken als voorbeelden.
6.2
Staafkrachten in een ligger
Zie figuur 6.1. De ligger is opgebouwd uit vijf staven. Er zijn vier knooppunten. De ligger wordt in einden ondersteund en belast met één puntlast ~F1 in het midden. De opdracht is de staafkrachten te bepalen. Ik ga dit oplossen in drie stappen. Maar eerst nummer ik de staven en benoem de knooppunten (zie figuur).
1. Stap 1. Zie figuur 6.2 . Ik bepaal de reactiekrachten ~Ra en ~Rb in de steunpunten door middel van poolfiguur en stangenveelhoek.
2. Stap 2. Zie figuur 6.3. Ik bekijk nu elk knooppunt afzonderlijk. In elke stang treden er inwendige krachten op. Op de knooppunten A, B en C werken er ook uitwendige krachten. Aangezien het geheel in evenwicht is moet elk knooppunt op zich in evenwicht
zijn. Dit wil zeggen dat de krachtenveelhoek in elk knooppunt moet gesloten zijn. 1 m A D B C F1 10 kN 1 2 3 5 4
Figuur 6.1: Staafkrachten in een ligger: opgave
1 m A D B C F1 10 kN 1 2 3 5 4 Ra Rb F1 Ra Rb
Figuur 6.2: Staafkrachten in een ligger: de reactiekrachten
Ik heb elk knooppunt afzonderlijk getekend met zijn in- en uitwendige krachten. Wanneer ik denk dat de staaf aan trek onderhevig is teken ik de vector van het knooppunt weg. In het geval van druk wijst de vector naar het knooppunt toe.
Ik neem staaf 1 als voorbeeld. Ik denk dat op staaf 1 druk uitgeoefend wordt. De pijlen van de vectoren ~1 wijzen daarom naar de knooppunten A en C. Het is nu duidelijk dat
1 m A D B C F1 10 kN 1 2 3 5 4 Ra Rb F1 Ra Rb Rb 4 5 F1 1 3 4 Ra 1 2 2 3 5 Ra Rb A B D C
Figuur 6.3: Staafkrachten in een ligger: krachten in de knooppunten
1 m A D B C F1 10 kN 1 2 3 5 4 Ra Rb F1 Ra Rb Rb 4 5 F1 1 3 4 Ra 1 2 2 3 5 Ra Rb Ra 1 2 2 A 1 Druk -Trek +
3. Stap 3. Zie figuur 6.4. Ik bekijk nu knooppunt A in detail. Het is in evenwicht. Dus de krachtenveelhoek moet gesloten zijn. ~Ra en de richtingen van ~1 en ~2 zijn gekend. Ik construeer een krachtendriehoek. De vectoren ~1 en ~2 zijn nu volledig bepaald. Ik krijg de bevestiging dat staaf 1 op druk belast is en staaf 2 op trek. Ik loop op deze manier alle knooppunten af.
6.3
Het Cremona-diagram
Het Cremona-diagram is een tekentechniek om de staafkrachten te bepalen. In figuur 6.5 leg ik de techniek stap voor stap uit.
1 m A D B C F 10 kN 1 2 3 5 4 Ra Rb F Ra Rb Ra Rb Ra Rb F Ra Rb 1 2 F Ra Rb 1 4 3 F Ra Rb 5 F A C B Ra Rb 2 5 3 F D 4 Ra Rb 5+ F 4- 1-2+ 3-1 2 3 4 5 6
Ik gebruik dezelfde opgave als in de vorige paragraaf.
1. Stap 1. Eerst bepaal ik de steunpuntreacties ~Ra en ~Rb. Ik teken de uitwendige krachtenveelhoek. Ik zal nu knooppunt per knooppunt in wijzerzin doorlopen.
2. Stap 2. Ik begin in knooppunt A. De kracht ~Ra is in evenwicht met ~1 (druk) en ~2 (trek).
3. Stap 3. Nu komt knooppunt C aan de beurt. Ik begin met de kracht ~F , dan komt stang 4 , 3 en tenslotte 1. De vector ~1 was reeds gekend en is nu tweemaal gebruikt (pijltjes in twee richtingen).
4. Stap 4. Nu komt knooppunt B aan de beurt. De kracht ~Rb wordt in evenwicht gehouden door ~5 (druk) en ~4 (trek). De vector ~4 was reeds gekend en is nu tweemaal gebruikt (pijltjes in twee richtingen).
5. Stap 5. Nu beschouw ik knooppunt D. Alle stangen die in D samenkomen werden reeds behandeld. De grootte van de vectoren is gekend. Ik controleer of de krachtenveelhoek gesloten is en de pijltjes tweemaal gebruikt zijn.
6. Stap 6. Ik breng alles samen en geeft met een + teken aan dat er een trekkracht in de staaf heerst of met een - teken dat het om een drukkracht gaat.
In de praktijk worden deze figuren natuurlijk niet afzonderlijk getekend, er is alleen het diagram uit stap 6. Noteer dat een Cremona-diagram er complex kan uitzien.
6.4
Kraan oplossen met knooppunten methode
1 m F1 F2 F3 F4 F5 10 kN
Figuur 6.6: Kraan: opgave
Figuur 6.6 toont de opgave die we hier zullen oplossen met de knooppunten methode. Zie figuur 6.7 voor de oplossing.
1. Stap 1. Ik benoem alle knooppunten en stangen. Ik bepaal de steunpuntreacties (deze actie heb ik niet in detail getekend).
2. Stap 2. Voor elk knooppunt teken ik de richting van de vectoren. Ik kies ook een zin voor de staafvectoren.
3. Stap 3. Ik begin bij knooppunt A, hier zijn slechts twee onbekenden. Ik teken de krachtendriehoek. Nu zijn ~1 en ~2 gekend.
4. Stappen 4 tot en met 9. Ik loop nu alle overblijvende knooppunten af.
1 m F1 F2 F3 F4 F5 10 kN F1 1 2 A 1 3 4 F2 B 2 3 5 6 C D F3 4 5 7 8 E F4 8 10 9 G F5 Rg 10 11 H Rh 6 7 9 11 G H E D B A C 1 2 3 4 5 6 7 8 9 10 11 B A C F2 F1 1 2 1 3 4 2 3 5 6 D F3 4 5 8 7 E F4 8 9 10 G F5 Rg 10 11 H Rh 6 7 9 11 Rg Rh
Figuur 6.7: Kraan: knooppunten methode
1 m F1 F2 F3 F4 F5 10 kN G H E D B A C 1 2 3 4 5 6 7 8 9 10 11 Rh 6 7 9 11 10 8 Rg F5 F4 F3 F2 F1 1 3 4 2 5 Rg Rh
Figuur 6.8: Kraan: Cremona-diagram
1. Stap 1. Ik benoem alle knooppunten en stangen. Ik bepaal de steunpuntreacties (deze actie heb ik niet getekend).
2. Stap 2. Ik teken de uitwendige krachtenveelhoek (ik startte met ~F5).
3. Stap 3. Ik begin in knooppunt G en bepaal−→10 en−→11. Ik neem ~Rg als eerste kracht en ga in wijzerzin rond het knooppunt.
4. Stap 4. Nu behandel ik knooppunt E en bepaal ~8 en ~9.
5. Stap 5. Knooppunt D heeft 3 onbekenden daarom neem ik eerst knooppunt H en bepaal ~6 en ~7.
6. Stap 6. Nu kan ik knooppunt D behandelen. Ik bepaal ~4 en ~5.
7. Stap 7. Ik kan nu kiezen tussen knooppunt B en C. Ik neem B en bepaal ~1 en ~3.
8. Stap 8. Nu behandel ik knooppunt C en bepaal ~2.
9. Stap 9. Tenslotte bekijk ik knooppunt A, alles is gesloten en alle stangen werden tweemaal ’gebruikt’. Ik ken alle krachten. De vraag of het trek- of drukkrachten zijn sla ik nu over.
6.6
Luifel
De figuur 6.9 stel een spant van een luifel voor. Bovenaan in A is het vakwerk met een trekstang aan de muur bevestigd en onderaan in B wordt het luifel ondersteun door een scharnieroplegging. Gevraagd wordt de staafkrachten te bepalen door middel van een Cremona-diagram.
A B 1 8 2 9 3 10 4 11 5 6 7 Q1 Q2 Q3 Q4 2 kN 1 m E D C F G
Figuur 6.9: Luifel: opgave
1. Stap 1. Zie figuur 6.10. Ik benoem de knooppunten en de stangen. Ik bepaal de reactiekrachten ~Ra en ~Rb door eerst de resultante ~Rv te bepalen door middel van poolfiguur en stangenveelhoek. Vervolgens splits ik ~Rv in ~Ra en ~Rb.
A B 1 8 2 9 3 10 4 11 5 6 7 Q1 Q2 Q3 Q4 2 kN 1 m E D C F G Q1 Q2 Q3 Q4 Rv Rv Ra Rb
Figuur 6.10: Luifel: reactiekrachten
2. Stap 2. Zie figuur 6.11. Ik teken de uitwendige krachtenveelhoek (ik begin bij ~Q1 en vervolg in wijzerzin).
A B 1 8 2 9 3 10 4 11 5 6 7 Q1 Q2 Q3 Q4 2 kN 1 m E D C F G Q1 Q2 Q3 Q4 Rb Ra Ra Rb
Figuur 6.11: Luifel: uitwendige krachtenveelhoek
3. Stap 3. Zie figuur 6.12. Ik teken nu het Cremona-diagram.
• Ik begin met knooppunt C en ~Q1. In wijzerzin kom ik stang 1 en stang 9 tegen. ~1 wijst van C weg (dus trek) en ~9 wijst naar C (dus druk).
• In knooppunt D zijn er twee onbekenden. Ik begin met ~Q2 en kom dan stang 2, 4 en 1 tegen. In stang 2 heerst er trek en in stang 4 heerst er druk. Stang 1 was reeds gekend.
• Ik los nu knooppunt F op (in E zijn er nog teveel onbekenden). Ik begin met stang 9, dan komt stang 4, stang 5 en stang 10. In stang 5 heerst er trek en in stang 10 heerst er druk.
• Nu komt knooppunt E aan de beurt. Ik begin met ~Q3, dan komt stang 3, stang 6, stang 5 en stang 2. In stang 3 heerst er trek en stang 6 heerst er druk.
• Ik behandel nu knooppunt G. Ik begin met stang 10, dan komt stang 6, stang 7 en stang 11. In stang 7 heerst er trek en in stang 11 heerst er druk.
tenslotte stang 8. In stang 8 heerst er een drukkracht.
• Als controle behandel ik knooppunt B.
A B 1 8 2 9 3 10 4 11 5 6 7 Q1 Q2 Q3 Q4 2 kN 1 m E D C F G Rv Ra Rb Q1 Q2 Q3 Q4 Rb Ra 9-1+ 2+ 4- 5+ 10- 11-3+ 6- 7+
8-Figuur 6.12: Luifel: Cremona-diagram
6.7
Vakwerkligger van een brug oplossen met Cremona-diagram
1 m
A B
Q/2 Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q/2
In figuur 6.13 heb ik een vakwerkligger van een brug getekend. De krachten Q1 tot en met Q7 zijn de resultanten van de eigen gewichten en zijn in elk knooppunt gelijk. Gevraagd wordt de krachten in de stangen te bepalen.
Aangezien de constructie symmetrisch is is het voldoende één helft te behandelen. Ik neem de linker helft en begin met het benoemen van de knooppunten en staven (zie figuur 6.14).
1 m A 1 B Q/2 5 8 12 2 Q1 6 9 13 3 Q2 7 10 14 4 Q3 7 11 15 4 Q4 6 10 15 3 Q5 5 9 14 2 Q6 8 13 1 Q7 12 Q/2 Ra Rb 1-12+ Q1 Q2 Q3 Q4 Q5 Q6 Q7 C D E F G Ra H I J
Figuur 6.14: Brug: uitwendige krachtenveelhoek
1. Stap 1. Zie figuur 6.14 . Ik bepaal de reactiekracht ~RA= ~Q/2 + ~Q1+ ~Q2+ ~Q3+ ~Q4/2. Nu teken ik de uitwendige krachtenveelhoek.
2. Stap 2. Zie figuur 6.15. Nu teken ik het Cremona-diagram.
• Ik begin met knooppunt A. Ik heb dit knooppunt vergroot weergeven. Ik bepaal de krachten in stangen 1 en 12.
• Als tweede knooppunt neem ik C en bepaal de krachten in stangen 8 en 5.
• Hoe het verder gaat kan je afleiden uit de figuur. Ik heb gebruik gemaakt van pijltjes en heb de staafnummers vermeld telkens ik ze tegenkwam. Knooppunt I heb ik niet getekend...
1 m A 1 B Q/2 5 8 12 2 Q1 6 9 13 3 Q2 7 10 14 4 Q3 7 11 15 4 Q4 6 10 15 3 Q5 5 9 14 2 Q6 8 13 1 Q7 12 Q/2 Ra Rb 1-12+ Q1 Q2 Q3 Q4 Q5 Q6 Q7 C D E F G Ra Ra Q/2 1-12+ 12+ A D C 1-H I J 8-5+ Knoop A Knoop C Kleuren legende
Figuur 6.15: Brug: Cremona-diagram knooppunt 1
1 m A 1 B Q/2 5 8 12 2 Q1 6 9 13 3 Q2 7 10 14 4 Q3 7 11 15 4 Q4 6 10 15 3 Q5 5 9 14 2 Q6 8 13 1 Q7 12 Q/2 Ra Rb 1-12+ Q1 Q2 Q3 Q4 Q5 Q6 Q7 C D E F G Ra H I J 8-5+ 12+ 2-13+ 8- 1-6+ 9-5+ 13+ 14+ 3- 9- 2-10+ 14+ 6+ 7- 4-15+ 10+ 3- 11- 4-Kleuren legende Knoop A Knoop C Knoop D Knoop E Knoop F Knoop G Knoop H Knoop J
6.8
Dakspant oplossen met Cremona-diagram
In figuur 6.17 heb ik een vakwerkligger van een dakspant getekend. De krachten Qc tot en met Qk zijn de resultanten van de eigen gewichten en zijn in elk knooppunt gelijk. Qa en Qb zijn beide de helft van Qc. Gevraagd wordt de krachten in de stangen te bepalen.
Aangezien de constructie symmetrisch is is het voldoende één helft te behandelen. Ik neem de linker helft en begin met het benoemen van de knooppunten en staven (zie figuur 6.18).
A B Qa Qc 2 kN 1 m E D C F G Qd Qe Qf Qg Qh Qk Qb H K L M N O P S
Figuur 6.17: Dakspant: opgave
A B 1 8 2 9 3 10 4 11 5 6 7 Qa Qc 2 kN 1 m E D C F G Qd Qe Qf Qg Qh Qk Qb H K L M N O P S 12 13 14 Ra Rb
A B 1 8 2 9 3 10 4 11 5 6 7 Qa Qc 2 kN 1 m E D C F G Qd Qe Qf Qg Qh Qk Qb H K L M N O P S 12 13 14 Ra Rb Qc Rb Ra Qd Qe Qf Qg Qh Qk Qb Qa 1-5+ 8- 2-9+ 6+ (11) 10- 3-11+ 13+ 7+ 4- 12-14+
Figuur 6.19: Dakspant: Cremona-diagram
1. Stap 1. Zie figuur 6.18 . Ik bepaal de reactiekrachten, teken de uitwendige krachten-veelhoek en benoem de knooppunten en stangen.
2. Stap 2. Zie figuur 6.19. Ik teken het Cremona-diagram voor het halve spant. Alleen het knooppunt F lijkt moeilijk, maar doordat de constructie er symmetrisch is kunnen we de staafkrachten bepalen.
6.9
Brugligger met zijdelingse belasting
Zie figuur 6.20 voor de opgave. Door de zijdelingse belasting ~Q1 zal de reactiekracht in de scharnieroplegging schuin staan. Bovendien is de belasting niet symmetrisch (slechts één helft is belast). Zoals steeds bepaal ik eerst de reactiekrachten. Daarvoor dien ik eerst de resultante te bepalen (zie figuur 6.21). Noteer dat ik de tekening hier slechts gedeeltelijk weergeef. Het snijpunt van de werklijnen van ~Ra, ~Rb en ~R ligt buiten mijn tekening.
1 m 2 kN G H K L A B Q1 Q2 Q3 Q4
Figuur 6.20: Brugligger met zijdelingse belasting: opgave
1 m 2 kN C D E F G H K L A B Q1 Q2 Q3 Q4 5 1 2 3 4 6 7 8 9 10 11 12 13 14 15 16 17 Ra Rb Q1 Q2 Q3 Q4 R 1 2 3 4 5 I II III IV V R Ra Rb 6 7 8 VI VII VIII
Het Cremona-diagram (zie figuur 6.22) :
1. Stap 1. Ik teken de externe krachtenveelhoek.
2. Stap 2. Ik start bij knooppunt A en bepaal de krachten in stangen 5 en 14.
3. Stap 3. Ik neem knooppunt C en bepaal de krachten in stangen 1 en 6.
4. Stap 4. Nu volgt knooppunt H en ik bepaal de krachten in stangen 7 en 15.
5. Stap 5. Ik ga naar knooppunt D en bepaal de krachten in stangen 2 en 8.
6. Stap 6. Ik neem knooppunt E en bepaal de krachten in stangen 3 en 9.
1 m 2 kN C D E F G H K L A B Q1 Q2 Q3 Q4 5 1 2 3 4 6 7 8 9 10 11 12 13 14 15 16 17 Ra Rb Q1 Q2 Q3 Q4 Ra Rb 5-14+ 1-6+ 7-15+ 2- 8- 9- 3-10+ 16+ 4-11- 12+ 13-17=0
7. Stap 7. Nu volgt knooppunt K en ik bepaal de krachten in stangen 10 en 16.
8. Stap 8. Ik neem knooppunt F en bepaal de krachten in stangen 4 en 11.
9. Stap 9. Ik neem knooppunt L en bepaal de krachten in stangen 12. Nu is de krach-tenveelhoek reeds gesloten, dus 17 is nul (staaf 17 noemen we een nulstaaf, het is een overbodige staaf).
10. Stap 10. Ik neem knooppunt G en bepaal de kracht in stang 13.
11. Stap 11. Ik controleer knooppunt B. De kracht in stang 13 heft ~Rb op. Ik krijg ook de bevestiging dat de kracht in stang 17 nul is.
6.10
De snedenmethodes van Culmann
Met een Cremona-diagram bepalen we de staafkrachten één voor één. De snedenmethodes stellen ons in staat om de kracht in een willekeurige staaf te bepalen. Het is ook een alternatief voor de Cremona-methode en om bij mobiele belastingen de invloedslijn te bepalen. Ik beperk mij tot de zuiver grafische methode van Culmann. Toch wil ik opmerken dat er gevallen zijn waarin deze methode niet werkt. Ik zal dit aantonen in volgend voorbeeld (zie figuur 6.23). Ik zal enkele staafkrachten bepalen van een kolom.
1 m 2 kN A B Q a b c
Het principe is eenvoud, men maakt een snede door het vakwerk en zondert een deel af. Dit deel moet in evenwicht zijn onder invloed van alle uitwendige krachten en de staafkrachten.
Ik heb drie sneden getekend.
1. Ik begin met snede a (zie figuur 6.24).
Ik heb het afgesneden deel afzonderlijk getekend. Voor duidelijkheid heb ik de staafkracht 20 wat verschoven. De uitwendige kracht ~Q en de staafkrachten −→20, −→21 en−→27 moeten evenwicht maken. Alleen −→20 en−→27 kunnen een gesloten krachtenveelhoek vormen met ~Q. Staaf 21 is een nulstaaf (er staat ook geen uitwendige kracht in knooppunt M).
2. Nu behandel ik snede b (zie figuur 6.25).
Terug teken ik het afgesneden deel afzonderlijk. Ik heb nu vier staafkrachten die evenwicht moeten maken met de uitwendige kracht. Deze snede is niet op te lossen met de Culmann methode.
3. Nu behandel ik snede c (zie figuur 6.26).
Ook hier kan ik geen staafkrachten bepalen bij gebrek aan voldoende gegevens.
1 m 2 kN A B Q a b c a Q L M 20 21 26 27 27 20 20 21 26 27 L M
1 m 2 kN A B Q a b c Q I J K L M N O P 14 15 16 17 19 20 21 22 23 24 25 26 27 28 29 18 b I J K N O P 14 15 16 17 22 23 24 25 28 29
Figuur 6.25: Staafkrachten met methode Culmann: snede b
1 m 2 kN A B Q a b c 1 2 3 c A C 1 2 3 6 8 9 Ra
Hoofdstuk 7
Invloedslijn en uiterste waarden
7.1
Inleiding
Indien een constructie onderworpen wordt aan een mobiele belasting zullen de krachten wijzigen met de verplaatsing van de last.
Indien men de verandering van een grootheid grafisch weergeeft voor de verschillende standen van de mobiele belasting dan ontstaat een figuur die men de invloedslijn noemt.
7.2
Invloedslijn ten gevolge van een puntlast
Zie figuur 7.1. De balk AB is ondersteund in A en B en heeft een lengte l. De last ~F beweegt over de balk van A naar B.
1 m 1 kN
F
A B
l
Figuur 7.1: Invloedslijn ten gevolge van een puntlast: opgave
1. De steunpunt reactiekrachten. Zie figuur 7.2. Ik ga eerst nagaan wat er met de steunpunt reactiekrachten ~Ra en ~Rb gebeurt.
• Als ~F in A staat is ~Ra= F . Wanneer ~F in B staat is ~Ra= O. In het punt X is:
Ra= l − x