1 Beschrijven van bewegingen met vectoren...3
1.1 De plaatsvector...3
1.2 Beweging...4
1.3 Verplaatsingsvector...4
1.4 De snelheidsvector...5
1.4.1 Gemiddelde snelheidsvector...5
1.4.2 Ogenblikkelijke snelheidsvector °...5
1.5 De versnellingsvector...6
1.5.1 De gemiddelde versnellingsvector...6
1.5.2 De ogenblikkelijke versnellingsvector °...6
1.5.3 Tangentiële en normaalversnelling °...7
1.6 Oefeningen ...8
1.6.1 Voorbeelden...8
1.6.2 Opgaves...10
2 Eéndimensionale bewegingen...11
2.1 Eenparig rechtlijnige bewegingen (ERB)...11
2.1.1 Definitie...11
2.1.2 Coördinaten...12
2.1.3 Diagrammen...12
2.2 Eenparig veranderlijke rechtlijnige bewegingen (EVRB)...13
2.2.1 Definitie...13
2.2.2 Coördinaten en bewegingsvergelijkingen...14
2.2.3 Diagrammen...15
2.3 Toepassing : de verticale worp...16
2.3.1 Beschrijving van de beweging...16
2.3.2 Berekenen van maximale hoogte...17
2.3.3 Berekenen van snelheid bij terugkeren op beginpositie...17
2.4 Oefeningen...18
2.4.1 Voorbeelden...18
2.4.2 Opgaves...22
3 Tweedimensionale bewegingen...24
3.1 Het onafhankelijkheidsprincipe...24
3.2 De horizontale worp...24
3.2.1 Beschrijving van de beweging...24
3.2.2 Berekenen van de dracht...25
3.3 De projectielbeweging (schuine worp)...26
3.3.1 Beschrijving van de beweging...26
3.3.2 De bewegingsvergelijkingen...27
3.3.3 Berekenen van de dracht...28
3.4 Oefeningen...28
3.4.1 Voorbeelden...28
3.4.2 Opgaven...31
4 De wetten van Newton...32
4.2 Tweede wet van Newton...36
4.2.1 Dynamische krachtwerking...36
4.2.2 Tangentiële en normaalkracht...37
4.3 Derde wet van Newton – Actie en reactie...37
4.4 Voorbeelden van krachten...38
4.4.1 Zwaartekracht nabij het aardoppervlak...38
4.4.2 Gewicht...38
4.4.3 Normaalkracht...38
4.4.4 Spankracht...39
4.4.5 Veerkracht...39
4.4.6 Wrijvingskracht tussen contactoppervlakken...40
4.4.7 Wrijvingskracht in een middenstof...43
4.5 Oefeningen...46
4.5.1 Algemene werkwijze...46
4.5.2 Voorbeelden...46
4.5.3 Opgaves...52
5 De universele wet van gravitatie...54
5.1 Historische ontwikkeling...54
5.1.1 Mesopotamiërs...54
5.1.2 Griekse astronomie in de oudheid...55
5.1.3 Ptolemaeus...55
5.1.4 De Middeleeuwen...57
5.1.5 Copernicus...57
5.1.6 Het conflict Galileï vs. de katholieke kerk...58
5.2 De wetten van Kepler voor planeetbewegingen...59
5.3 De universele gravitatiewet van Newton...61
5.4 Oefeningen...64
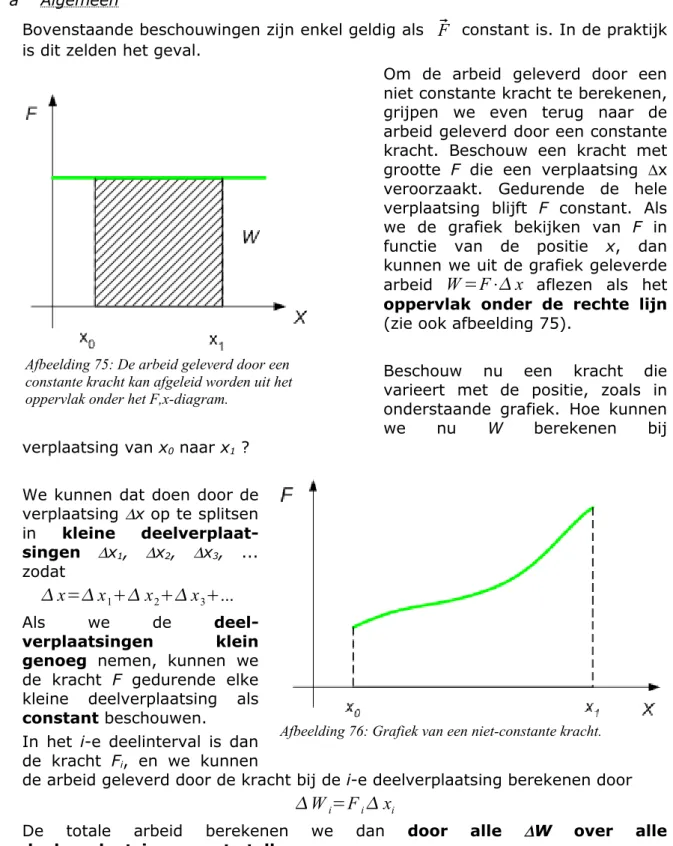
6 Arbeid en Energie...65
6.1 Arbeid...65
6.1.1 Arbeid geleverd door een constante kracht...65
6.1.2 Arbeid geleverd door niet constante krachten...65
6.1.3 Vermogen...65
6.2 Kinetische energie...65
6.3 Potentiële energie...65
6.3.1 Conservatieve krachten...65
6.3.2 Arbeid-energie theorema voor conservatieve krachten...65
6.4 Behoud van energie...65
6.4.1 Arbeid-energie theorema met niet-conservatieve krachten...65
6.4.2 Equivalentie van massa en energie...65
1 Beschrijven van bewegingen met vectoren
1.1 De plaatsvector
De positie van je huis ten opzichte van het punt waar je je nu bevindt kan aangegeven door te zeggen : “mijn huis bevindt zich ten opzichte van waar ik nu sta exact vijf kilometer naar het noord-westen”.
Je geeft een
• aangrijpingspunt (“waar ik nu sta”), • een grootte (“vijf kilometer”)
• een zin en een richting (“naar het noord-westen”).
Wat je eigenlijk doet is de positie beschrijven met behulp van een vector.
De positie van een voorwerp ten opzichte van een waarnemer kan beschreven worden door middel van een vector. Deze vector noemen we plaats- of
positievector van het voorwerp ten opzichte van de waarnemer.
We noteren de plaatsvector als
r
.Als we een orthonormaal
assenstelsel invoeren met de waarnemer in de oorsprong,
kunnen we de plaatsvector beschrijven met behulp van
coördinaten.
In deze cursus gaan we ons beperken tot bewegingen in één vlak, dus volstaat het ons te beperken tot twee assen (X,Y) en bijgevolg ook twee coördinaten. Zij
e
x ene
y eenheidsvectorenin resp. de richting van de X-as en de Y-as. Dan kan de plaatsvector van een voorwerp geschreven worden als :
r=x⋅
e
x
y⋅
e
y
r= x , y
Het koppel reële getallen (x,y) zijn dan de coördinaten van het voorwerp met plaatsvector
r
.Hoeveel coördinaten heb je nodig als je de positie van een voorwerp wil beschrijven in de ruimte in plaats van in een vlak ?
Afbeelding 1: Plaatsvector van een voorwerp.
1.2 Beweging
Een voorwerp is in beweging ten opzichte van een waarnemer als het voorwerp op verschillende tijdstippen een verschillende positie inneemt.
Als we de positie beschrijven met behulp van een plaatsvector, kunnen we bijgevolg zeggen dat een voorwerp in beweging is, als het op verschillende tijdstippen een verschillende plaatsvector heeft. De plaatsvector is met
andere woorden een functie van de tijd.
We noteren de plaatsvector van het voorwerp op een tijdstip t als
r t
.De verzameling van alle plaatsvectoren ingenomen door het voorwerp in een zeker tijdsinterval, noemen we de
baan van het voorwerp.
Als de plaatsvector wijzigt in functie van de tijd, dan zullen
ook de coördinaten wijzigen in functie van de tijd. We
noteren de coördinaten van het voorwerp een tijdstip t als
r t= x t , y t
1.3 Verplaatsingsvector
Beschouw een voorwerp in beweging. Op tijdstip t0 is zijn plaatsvector
r t
0
. Op een later tijdstip t1 is zijn plaatsvectorr t
1
.We definiëren nu de verplaatsingsvector
r
in het tijdsinterval
t=t
1−
t
0 als r=r t
1
−r t
0
We kunnen ook werken met coördinaten: zij
r t
0=
x t
0
, y t
0
enr t
1=
x t
1
, y t
1
, dan worden de coördinaten van de verplaatsingsvector gegeven door : r= x , y
r= x t
1−
x t
0
, y t
1−
y t
0
Hoe kan je, als de coördinaten kent van het begin- en eindpunt, de afstand berekenen waarover het voorwerp verplaatst is ?
Wat is de eenheid van de coördinaten van de verplaatsingsvector ? Is deze afstand hetzelfde als de afgelegde weg ∆ s ?
Afbeelding 3: Plaatsvectoren op verschillende tijdstippen van een voorwerp in beweging.
Afbeelding 4: De verplaatsingsvector
1.4 De snelheidsvector
1.4.1 Gemiddelde snelheidsvector
Als een voorwerp zich gedurende een tijdsinterval
t=t
1−
t
0 heeftverplaatst langs een
verplaatsingsvector
r=r t
1−r t
0
, dan definiërenwe de gemiddelde
snelheidsvector gedurende dat
tijdsinterval als :
v
m=
r
t
v
m=
r t
1−
r t
0
t
1−
t
0Merk op dat de gemiddelde
snelheidsvector steeds dezelfde zin en richting heeft als de verplaatsingsvector. De coördinaten van de snelheidsvector worden gegeven door
v
m=
v
m , x, v
m , y
v
m=
x
t
,
y
t
v
m=
x t
1−
x t
2
t
1−
t
2,
y t
1−
y t
2
t
1−
t
2
Wat is de eenheid van de coördinaten van de gemiddelde snelheidsvector ?
De gemiddelde afstand waarover het voorwerp per tijdseenheid verplaatst wordt, wordt gegeven door de grootte van de gemiddelde snelheidsvector :
∥
v
m∥=
v
x2
v
2y∥
v
m∥=
∥
r∥
t
Verwar de snelheidsvector niet met de baansnelheid
v=
s
t
uit de cursus vanhet vierde jaar ! Wat zijn de verschillen ?
1.4.2 Ogenblikkelijke snelheidsvector °
De snelheidsvector gedurende een gegeven tijdsinterval blijft bij realistische bewegingen niet constant, maar wisselt continu. Om een beweging exact te beschrijven, zou je op elk moment de snelheidsvector
v t
moeten kennen. We definiëren de ogenblikkelijke snelheidsvector als de gemiddelde snelheidsvector over een oneindig klein tijdsinterval.
v t=lim
t 0r t t−r t
t
Op bijstaande figuur zien we hoe de richting van de gemiddelde snelheidsvector meer en meer de raaklijn aan de baan benadert, als we tijdsinterval verkleinen.
1.5 De versnellingsvector
1.5.1 De gemiddelde versnellingsvector
Als de snelheid niet constant blijft, kunnen we een gemiddelde
versnellingsvector definiëren als volgt: zij
v t
o
de snelheid op tijdstip t0, env t
1
de snelheid op tijdstip t1, dan is de gemiddelde versnellingsvectorgegeven door :
a
m=
v
t
a
m=
v t
1−
v t
0
t
1−
t
0De coördinaten van de gemiddelde versnellingsvector worden gegeven door :
a
m=
a
m , x, a
m , y
a
m=
v
x
t
,
v
y
t
a
m=
v
x
t
1−
v
x
t
2
t
1−
t
2,
v
y
t
1−
v
y
t
2
t
1−
t
2
Wat is de eenheid van de coördinaten van de gemiddelde versnellingsvector ?
1.5.2 De ogenblikkelijke versnellingsvector °
Net zoals de snelheidsvector gedurende een tijdsinterval niet constant hoeft te blijven, is dit ook het geval met de versnellingsvector. Analoog als de ogenblikkelijke snelheidsvector definiëren we de ogenblikkelijke versnellingsvector als de gemiddelde versnellingsvector over een oneindig klein tijdsinterval :
a t =lim
t 0v t t−v t
t
Als we in wat volgt spreken over “de snelheid”, bedoelen we daar altijd de ogenblikkelijke snelheid mee, tenzij expliciet anders vernoemd.
1.5.3 Tangentiële en normaalversnelling °
Men kan de ogenblikkelijke versnellingsvector
a t
ontbinden in● een component evenwijdig met de ogenblikkelijke snelheidsvector, ook wel de tangentiële (rakend aan de baan) component
a
t
t
of genoemd● en een component loodrecht op de ogenblikkelijke snelheidsvector, de normaalcomponent
a
n
t
genoemd.Zo dat
a
t
t
a
n
t=at
.De tangentiële versnelling is verantwoordelijk voor de wijziging in grootte van de snelheidsvector.
De normale component is verantwoordelijk voor de wijziging van richting van de snelheidsvector.
Kan de grootte van de snelheidsvector constant blijven terwijl de versnellingsvector niet de nulvector is ? Verklaar !
Afbeelding 7: Plaats-, ogenblikkelijke snelheids-, en versnellingsvector op drie verschillende tijdstippen.
Afbeelding 8: ontbinding in tangentiële en normaalcomponent.
1.6 Oefeningen
1.6.1 Voorbeelden
a Voorbeeld 1
Een boot vertrekt vanaf de kade en vaart gedurende 15 minuten met een gemiddelde snelheidsvector gegeven door
v
1=
3
m
s
, 4
m
s
, wijzigt zijn koers, envaart dan gedurende 30 minuten met een snelheidsvector gegeven door
v
2=−2
m
s
, 3
m
s
. Bereken de afstand tussen zijn vertrekpunt en zijn positie na15 minuten en na 45 minuten.
Gegevens :
We kiezen de oorsprong van ons assenstelsel in het vertrekpunt, en kiezen als begintijdstip t0 = 0s.
t
0=0 s , t
1=900 s ,t
2=
2700 s
r t
0=0 m , 0 m
v
1=
3
m
s
, 4
m
s
v
2=−2
m
s
, 3
m
s
Oplossing :We bepalen eerst de positie op t1 :
r=
v
1⋅
t
r
1=
v
1⋅
t
x t
1
, y t
1=
v
m , x ,1⋅
t
1−
t
0
, v
m , y,1⋅
t
1−
t
0
x t
1
, y t
1=3
m
s
⋅
900 s ,5
m
s
⋅900 s
x t
1
, y t
1=2700m , 3600m
De afstand tussen het vertrekpunt en de positie op t1 wordt gegeven door :
∥r t
1∥=
x
2
t
1
y
2
t
1
∥
r t
1∥=
2700 m
23600 m
2∥
r t
1∥=4500 m
b Voorbeeld 2De beweging van een voorwerp wordt beschreven door volgende vergelijkingen :
r t= x t=5⋅t3, y t =−4⋅t
2
t
.● Bepaal de positie van het voorwerp na 2s en na 4 s.
● Bereken de verplaatsingsvector en de afstand waarover het voorwerp
● Bereken de gemiddelde snelheidsvector tussen 2s en 4s. Bepaal eveneens
de grootte van de gemiddelde snelheidsvector.
Gegeven :
t
0=0s , t
1=2s , t
3=4s
x t=5⋅t3
y t =−4⋅t
2
t
¿
Gevraagdr t
1
, rt
2
,r ,
v
m,∥
v
m∥
Oplossingr t
1=
x t
1
, y t
1
r t
1=
x t=5
m
s
⋅
t3 m , y t=−4
m
s
2⋅
t
2
t
m
s
r 2 s= x t=5
m
s
⋅2 s3 m , y t=−4
m
s
2⋅2 s
2
2 s
m
s
r 2 s= x t =13 m , y t=−12 m
analoog :r 4 s = x t =23 m , y t =−60 m
Berekenen we de verplaatsingsvector : r=r 4s−r 2s
r= x 4s− x 2s , y 4s− y 2s
r=10m ,−48m
De afstand waarover voorwerp verplaatst is
∥
r∥=
x
2
y
2∥
r∥=
10 m
2−
48 m
2
∥
r∥=49,03 m
De gemiddelde snelheidsvector
v
m=
r
t
v
m=
x
t
,
y
t
v
m=5
m
s
,−24
m
s
De grootte van de gemiddelde snelheidsvector
∥
v
m∥=
v
2x
v
2y∥
v
m∥=
5
m
s
2−24
m
s
2∥
v
m∥=
24,52
m
s
1.6.2 Opgaves
1. Een voorwerp bevindt zich op tijdstip t0 in een positie met coördinaten
(3m,4m). 5 s later bevindt het voorwerp zich in een positie met coördinaten (5m,2m). Maak een schets van de posities en bereken de coördinaten van de verplaatsingsvector en de gemiddelde snelheidsvector. Bereken eveneens over welke afstand het voorwerp verplaatst is.
2. Bepaal de coördinaten van de positie op t = 0 s, t = 3 s en t = 6 s van een voorwerp waarvan de bewegingsvergelijking gegeven wordt door (x(t) = t + 2, y(t) = -2t + 5). Maak eveneens een schets. Welke figuur beschrijft de baan ? Bepaal de gemiddelde snelheidsvector gedurende de eerste drie seconden, tussen 3 s en 6 s, en tussen 0 s en 6 s . Wat kan je concluderen ?
3. Een voertuig vertrekt vanuit een beginpositie met coördinaten (3m, 3m) en moet naar een eindpositie met coördinaten (18m, -12m). Bereken de gemiddelde snelheidsvector waarmee het voertuig moet bewegen wil het 5 minuten na zijn vertrek op de eindpositie aankomen.
2 Eéndimensionale bewegingen
2.1 Eenparig rechtlijnige bewegingen (ERB)
2.1.1 Definitie
Een éénparig rechtlijnige beweging (ERB) is een beweging waarbij de snelheidsvector
v
constant is.Als
v
constant is, dan geldt voor elk tijdsinterval ∆t :
v =
r
t
r=v⋅t
Waarmee de plaatsvector op een willekeurig moment t gegeven wordt door :
r t =
r
0v⋅ t
r t=
r
0
v⋅t−t
0
met
r
0 de plaatsvector op begintijdstip t0.De vergelijking die de plaatsvector geeft op een willekeurig tijdstip t, noemen we de positie-vergelijking.
Bij een dergelijke beweging is de baan een rechte, nl. de richting van de snelheidsvector.
Tevens volgt uit bovenstaande vergelijkingen :
∥ r∥=∥v∥⋅ t
of de afstand waarover het voorwerp dat een eenparig rechtlijnige beweging uitvoert verplaatst is, is recht evenredig met het tijdsverloop.
Afbeelding 9: Alle posities ingenomen door een voorwerp dat een ERB beschrijft liggen op één rechte.
2.1.2 Coördinaten
Als we een coördinatenstelsel invoeren om een ERB te beschrijven, kiezen we meestal de X-as volgens de richting van de snelheidsvector (en dus in de richting van de baan). Op deze manier kan de beweging volledig beschreven worden met behulp van één (X-)coördinaat. De Y-coördinaat is dan op elk ogenblik gelijk aan nul, en laten we verder buiten beschouwing.
De positievergelijking in coördinaten wordt dan :
r t= x t= x
0
v
x⋅
t−t
0
, y t=0
Of kortweg :x t =x
0
v
x⋅
t−t
0
Hoe ziet de beweging eruit als vx negatief is ?
Hoe kan je deze beweging vergelijken met de eenparige beweging die je vorig jaar gezien hebt ?
2.1.3 Diagrammen
a x,t -diagram
Met behulp van bovenstaande vergelijking kunnen we de x-coördinaat uitzetten als functie van de tijd in een x,t-diagram. Net als bij het s,t diagram dat je vorig jaar gezien hebt, zet je bij het x,t-diagram altijd de tijd op de horizontale as, en de positie op de verticale as. Het x,t-diagram van een ERB is een schuine rechte.
Hoe kan je uit het x,t -diagram de snelheid aflezen ?
Hoe ziet het x,t diagram eruit als vx
negatief is ?
Afbeelding 11: x,t diagram van een ERB Afbeelding 10: Door de X-as in de bewegingsrichting te kiezen,
b V x,t - diagram
Bij een ERB is de snelheidsvector constant, en bijgevolg zijn ook de coördinaten van snelheidsvector constant. Het vx, t-diagram is dus
een horizontale rechte.
Hoe ziet het vx,t-diagram eruit als
de vx negatief is ?
Hoe kan je uit het vx,t diagram de
afgelegde weg aflezen ?
2.2 Eenparig veranderlijke rechtlijnige bewegingen (EVRB)
2.2.1 Definitie
Een éénparig veranderlijke beweging (EVRB) is een beweging waarbij ● de versnellingsvector constant is,
● de richting van de versnellingsvector gelijk is aan de richting van de snelheidsvector.
De beweging is éénparig versneld als de versnellings- en snelheidsvector dezelfde zin hebben.
De beweging is éénparig vertraagd als de versnellings- en de snelheidsvector tegengestelde zin hebben.
Afbeelding 12: vx,t diagram van een ERB
Als
a
constant is, geldt op elk ogenblik t :
a=
v
t
v =a⋅t
waardoor de snelheidsvector op een gegeven tijdstip t gegeven wordt door :
v t=
v
0a⋅ t
v t=
v
0a⋅t−t
0
De vergelijking die de snelheidsvector geeft op een willekeurig tijdstip t, noemen we de snelheidsvergelijking.
Vermits de richting van de snelheidsvector niet wijzigt, wijzigt ook de richting van de baan niet. De baan van een voorwerp dat een EVRB beschrijft is bijgevolg een rechte.
De plaatsvector bepalen is echter niet meer zo eenvoudig, en daarvoor gaan we direct over op coördinaten.
2.2.2 Coördinaten en bewegingsvergelijkingen
Net zoals bij de ERB kiezen we de X-as volgens de bewegingsrichting. Omdat de beweging rechtlijnig is, zal de Y-coördinaat niet wijzigen en die laten we bijgevolg buiten beschouwing.
De snelheidsvergelijking in coördinaten wordt :
v
x
t=v
x ,0
a
x⋅
t−t
0
We gaan nu proberen een vergelijking op te stellen om de x-coördinaat op een willekeurig tijdstip t te bepalen.
Uit de definitie van gemiddelde snelheid volgt dat
x t =x
0
v
m , x
t ⋅t−t
0
met de gemiddelde snelheid na een tijd t.
Vermits uit de snelheidsvergelijking volgt dat vx een lineair aangroeiende
grootheid is, kunnen we de gemiddelde snelheid berekenen als volgt :
v
m , x
t=
v
0, x
v
x
t
2
waardoorx t =x
0
v
0, x
v
x
t
2
⋅
t−t
0
x t =x
0
v
0, x
v
x ,0
a
x⋅
t−t
0
2
⋅
t−t
0
x t =x
0
v
0, x⋅
t−t
0
1
2
a
x⋅
t−t
0
2Deze laaste uitdrukking geeft de x-coördinaat op tijdstip t van een voorwerp dat een EVRB beschrijft met beginsnelheid v0, vertrekkende op positie x0, en is de
positievergelijking van de EVRB. Samengevat :
De bewegingsvergelijkingen van een voorwerp dat een EVRB beschrijft zijn bijgevolg :
a
x
t=a
x=
const.
v
x
t=v
0, x
a
x⋅
t−t
0
x t =x
0
v
0, x⋅
t−t
0
1
2
a
x⋅
t−t
0
2Merk op dat als de versnelling nul is, bovenstaande vergelijkingen identiek zijn aan de bewegingsvergelijkingen van een ERB.
2.2.3 Diagrammen
a a,t -diagram
Bij een eenparig veranderlijke beweging is de versnelling bij definitie een constante. Het a,t-diagram is bijgevolg een horizontale rechte. Hiernaast is de grafiek afgebeeld van een eenparig versnelde beweging.
Wat wordt dit diagram in geval van een eenparig vertraagde beweging ?
b v,t-diagram
We zien in de bewegingsvergelijkingen dat de snelheid lineair toe- of afneemt met de
tijd. Het v,t – diagram is bijgevolg een schuine rechte. Hieronder is het v,t – diagram afgebeeld voor zowel een versnelde, als een vertraagde beweging.
Hoe kan je in het v,t -diagram de afgelegde weg aflezen ?
Afbeelding 15: a,t -diagram van een eenparig versnelde beweging.
Afbeelding 16: v,t - diagram van een eenparig versnelde beweging.
Afbeelding 17: v,t - diagram van een eenparig vertraagde beweging.
wanneer dan niet meer ? c x,t – diagram
Uit de bewegingsvergelijkingen volgt dat de grafiek die de positie x geeft in functie van de tijd t een parabool is (kwadratische vergelijking). We moeten echter wel een onderscheid maken tussen een versnelde en een vertraagde beweging. In onderstaande figuur is het x,t-diagram weergegeven voor beide gevallen.
Hoe lees je af in het x,t-diagram van de vertraagde beweging waar de snelheid nul wordt ?
In welk gedeelte, in het diagram van de vertraagde beweging, is de beweging effectief “vertraagd” ? Welke beweging hebben we in het andere gedeelte ?
2.3 Toepassing : de verticale worp
2.3.1 Beschrijving van de beweging
Een verticale worp definiëren als de beweging beschreven door een voorwerp dat loodrecht omhoog gegooid wordt met een beginsnelheid v0, vanop een
beginhoogte y0.
Het is een eendimensionale beweging, en we kiezen de Y-as volgens de bewegingsrichting, met zin naar boven (volgens de zin van de beginsnelheid) toe.
Eens het voorwerp de hand verlaten heeft, werkt enkel de zwaartekracht op het voorwerp, en zal het voorwerp eenparig vertragen met
a
y=−
g=−9,81
m
s
2Afbeelding 18: x,t diagram voor een EVRB, zowel voor een versnelde (links) als voor een vertraagde (rechts) beweging.
We verwaarlozen hierbij eventuele wrijving. Het voorwerp zal een maximale hoogte (top) bereiken, om dan eenparig versneld weer terug te keren naar zijn beginhoogte (en eventueel verder te vallen).
We willen nu drie zaken berekenen :
● Wat is de maximaal bereikte hoogte ? ● Hoelang duurt het tot het voorwerp terug
op beginhoogte is ?
● Wat is de snelheidscomponent bij terugkeer op beginhoogte ?
2.3.2 Berekenen van maximale hoogte
De verticale worp is een EVRB met beginsnelheid v0 en versnelling a = -g. De
bewegingsvergelijkingen worden bijgevolg :
v
y
t=v
0−
g⋅t
y t= y
0
v
0⋅
t−
1
2
g⋅t
2Op maximale hoogte is de snelheid van het voorwerp 0 m/s. Hiermee kunnen we het tijdstip t1 berekenen waarop het voorwerp de maximale hoogte bereikt.
v
y
t
1=
0
m
s
v
0−
g t
1=0
m
s
t
1=
v
0g
De maximale hoogte is de positie op het moment dat de snelheid nul wordt.
y
max=
y t
1
y
max=
y
0
v
0⋅
t
1−
1
2
g⋅t
2y
max=
y
0
v
0⋅
v
0g
−
1
2
g⋅
v
0g
2y
max=
y
0
1
2
v
02g
2.3.3 Berekenen van snelheid bij terugkeren op beginpositie
Noemen we t2 het tijdstip waarop het voorwerp terug is op zijn beginpositie. Met
andere woorden :
y t
2=
y
0y
0=
y
0
v
0⋅
t
2−
1
2
g⋅t
2 2 Afbeelding 19: Beginsituatie bij verticale worp : positie, snelheid en versnelling.Dit is een vierkantswortelvergelijking met twee oplossingen, namelijk
t
2=0 s
oft
2=
2 v
0g
(reken zelf na !).Hoe moet je die twee oplossingen interpreteren ?
We zien dat het twee keer zo lang duurt om terug op beginhoogte te komen, dan dat het duurt om maximale hoogte te bereiken.
De snelheid bij terugkeer op beginhoogte wordt dan gegeven door
v t
2=
v
0−
g⋅t
2v t
2=
v
0−
g⋅
2v
0g
v t
2=−
v
0De snelheid bij terugkeer op beginhoogte is bijgevolg gelijk in grootte aan de beginsnelheid, maar tegengesteld gericht.
2.4 Oefeningen
2.4.1 Voorbeelden
a Voorbeeld 1
Opgave :
Een trein rijdt tegen 72 km/h over een recht stuk spoorweg naar het station toe. 200 m voor het perron begint te trein te remmen. Met welke vertraging moet de trein remmen om aan het perron tot stilstand te komen ?
Tekening :
Een dergelijke oefening begin je altijd met een tekening, waarin je een schets maakt van de situatie, en alle relevante grootheden en parameters aanduidt en benoemt. De artistieke waarde van de schets is van geen belang, wél de duidelijkheid en volledigheid waarmee het je kan helpen het gevraagde te berekenen.
Op de figuur staan aangeduid :
● De situatie op het moment t0 dat de trein begint te remmen, met aanduiding van
beginsnelheid en vertraging.
● De situatie op het moment t1 dat de trein stilstaat (snelheid is nul).
● Een X -as met aanduiding van de oorsprong.
Eens de schets gemaakt, kan je die gebruiken om zoveel mogelijk gegevens te noteren.
Dikwijls zullen er een aantal gegevens opduiken die niet letterlijk in de opgave staan, maar die door bvb. keuze van het assenstelsel naar voor zullen komen.
Gegevens:
t
0=
0 s
v
0=2,00⋅10
1m
s
x
0=
x t
0=0 m
v t
1=0
m
s
x t
1=2,00⋅10
2m
Merk op dat we de gegevens overzichtelijk gerangschikt hebben in twee kolommen, één met de gegevens betreffende de beginsituatie, één met de gegevens betreffende de eindsituatie.
Gevraagd :
Noteer altijd expliciet het gevraagde, zodat je duidelijk weet wàt je aan het zoeken bent.
a=?
Oplossing :Het vraagstuk is duidelijk een toepassing van een eenparig vertraagde beweging. We vertrekken bijgevolg van de bewegingsvergelijkingen van een eenparig vertraagde beweging, en zullen bekijken over welke grootheden we beschikken en welke onbekenden we zullen moeten bepalen.
v t
1=
v
0
a⋅t
1=0
m
s
x t
1=
v
0⋅
t
1
1
2
a⋅t
1 2In bovenstaande vergelijkingen zijn alle grootheden waarvan gegeven is dat ze nul zijn al weggelaten. Als we de gegevens vergelijken, is het duidelijk dat we met twee onbekenden
zitten, nl. t1 en a. We hebben echter ook twee vergelijkingen, dus in theorie zou dit perfect
oplosbaar moeten zijn. We gebruiken nu de eerste vergelijking om t1 te elimineren in de
tweede vergelijking, en zo a te bepalen.
t
1=−
v
0a
Invullen in de tweede vergelijking geeft :
x t
1=
v
0⋅−
v
0a
1
2
a⋅−
v
0a
2x t
1=−
1
2
v
02a
a=−
1
2
v
02x t
1
We hebben nu algebraïsch het gevraagde in functie van het gegeven bepaald. Het is ten zeerste belangrijk dat je eerst alles zo ver mogelijk algebraïsch uitwerkt vooraleer je cijfers gaat invullen !!! Dit vermijdt rekenfouten, is overzichtelijker, en geeft veel duidelijker de gevolgde redenering weer. Het maakt het ook veel gemakkelijker een eventuele fout op te sporen, mocht je je ergens vergist hebben en niet het gewenste resultaat bekomen.
Eens je het gevraagde hebt in functie van het gegeven, kan je de gegevens invullen en het resultaat berekenen. Zet bij elke stap van je berekeningen ook je eenheden ! Als je eenheden niet kloppen, ben je al zeker dat je ergens een reken- of redeneerfout gemaakt hebt !
a=
−
2,00⋅10
1m
s
22⋅2,00⋅10
2m
a=
−4,00⋅10
2m
2s
24,00⋅10
2m
a=−1
m
s
2Ten slotte formuleer je een korte, maar duidelijke antwoordzin :
Antwoord:
De trein moet afremmen met een vertraging van
−1
m
s
2b Voorbeeld 2
Een politiewagen rijdt tegen 90 km/h over een recht stuk autosnelweg, als hij gepasseerd wordt door een hardrijder die voorbijraast met een snelheid van 160 km/h. Op het moment dat de hardrijder hem passeert, versnelt de politiewagen met 2,00 m/s². Als de hardrijder tegen dezelfde snelheid blijft rijden,hoe lang zal het duren vooraleer de politiewagen de hardrijder inhaalt, en welke afstand is daarbij afgelegd ? Tekening : Gegevens :
t
0=0 s
x
A
t
0=
x
B
t
0=0 m
v
0, A=2,50⋅10
1m
s
v
0, B=4,44⋅10
1m
s
=
v
B
t
a
A=
2,00
m
s
2x
A
t
1=
x
B
t
1
v
B
t
1=
4,44⋅10
1m
s
Gevraagd :
t
1=
? ; x
A
t
1=
?
Oplossing :x
A
t
1=
x
B
t
1
v
0, A⋅
t
1
1
2
a
At
1 2=
v
0, B⋅
t
1t
1⋅[
v
0, A−
v
0, B
1
2
a
At
1]=0
Oplossen naar t1 geeftt
1=0 s
oft
1=
2v
0, B−
v
0, A
a
ADe eerste oplossing is het beginstijdstip, de tweede oplossing is het moment waarop de politieauto de snelheidsovertreder inhaalt.
Vullen we de gegevens in :
t
1=
2⋅4,44⋅10
1m
s
−2,50⋅10
1m
s
2,00
m
s
2t
1=1,94⋅10
1s
Berekenen we nu de afgelegde weg :x
A
t
1=
x
B
t
1=
4,44⋅10
1m
s
⋅
1,94⋅10
1s
x
A
t
1=8,61⋅10
2m
Antwoord :
De politieauto haalt de hardrijder in na 19,4 s, en ze hebben dan 861 m afgelegd.
2.4.2 Opgaves
1. Een auto rijdt tegen een snelheid van 60,0 km/h. Op een bepaald ogenblik begint hij te versnellen zodat in de 30,0 s nadien een afstand van 1400 m afgelegd wordt.
a) Bereken de grootte van de versnelling.
b) Hoe groot is de snelheid van de auto na die 30,0 s ?
2. Een voorwerp, dat eenparig veranderlijk rechtlijnig beweegt, bevindt zich op t = 0 s in een punt 30 m links van de waarnemer. Het heeft een beginsnelheid van 20 m/s weg van de waarnemer en een versnelling van 4,0 m/s² naar de waarnemer toe.
a) Wanneer is zijn snelheid 0 m/s ? b) Waar bevindt het zich dan ?
c) Wanneer is de beweging vertraagd, en wanneer is ze versneld ?
3. Een auto rijdt tegen 90 km/h op een autobaan, als de bestuurder plots 300 m verder een file opmerkt. Met welke vertraging moet de bestuurder remmen om een botsing te vermijden
a) Als de auto's in de file stilstaan ?
b) Als de auto's stapvoets rijden tegen 15 km/h ?
4. Een trein rijdt tegen 120 km/h, als de treinbestuurder het signaal krijgt dat er 1000 m voor hem een andere trein rijdt, met een snelheid van 90 km/h. In welke mate moet hij zijn trein vertragen, wil hij op 200 m achter de voorliggende trein de weg vervolgen ?
5. Het snelheidsdiagram van een racewagen op een recht gedeelte van zijn parcours vertoont een verloop zoals aangegeven in afbeelding 22. Bepaal:
a) De gemiddelde snelheid gedurende die 8 s.
b) De positieverandering gedurende die 8 s.
6. De grafiek stelt de snelheidscomponent voor van een puntmassa die beweegt langs de x-as. Op welke tijdstippen is de puntmassa het verst verwijderd van zijn positie op tijdstip t = 0 s ?
a) t = 2 s; b) t = 3 s; c) t = 4 s;
d) t = 2 s en t = 4 s;
e) geen van bovenstaande, het is op t = ______ s
Afbeelding 22: Grafiek oefening 5
7. Een tennisspeler gooit een tennisbal zo hard als hij kan op de grond. We verwaarlozen de wrijving met de lucht. Van de versnelling a van de bal nadat de speler hem heeft los gelaten kun je zeggen dat :
a) De grootte van de versnelling a van de bal voor het stuiten op de grond is groter dan g en is na het stuiten op de grond kleiner dan g. b) De grootte van de versnelling a van de bal voor het stuiten op de
grond is groter dan g en is na het stuiten op de grond gelijk aan g. c) De grootte van de versnelling a van de bal is zowel voor het stuiten op
de grond als na het stuiten op de grond gelijk aan g.
d) De grootte van de versnelling a van de bal voor het stuiten op de grond gelijk aan g maar is na het stuiten op de grond afhankelijk van de hardheid van de grond.
8. Een pijl wordt verticaal van de grond omhoog geschoten en bereikt na 2,5 s het hoogste punt. Bereken de startsnelheid en de bereikte hoogte. 9. Uit een punt 45,0 m boven de begane grond wordt een steen van 0,30 kg
verticaal omhooggeworpen met een snelheid van 42,0 m/s. Bereken: a) De door het lichaam bereikte hoogte boven de grond;
b) De tijd nodig om de grond te bereiken; c) De snelheid bij het bereiken van de grond.
10.Vanop een 300 m hoge mast valt een steen vrij naar beneden. Op hetzelfde ogenblik, dat de steen in vrije val vertrekt, werpt iemand een tweede steen verticaal de lucht in met een beginsnelheid van 60,0 m/s. a) Op welke hoogte passeren de stenen elkaar ?
3 Tweedimensionale bewegingen
3.1 Het onafhankelijkheidsprincipe
We houden twee gelijke voorwerpen op dezelfde hoogte boven de grond. Eén voorwerp laten we recht naar beneden vallen, tegelijkertijd gooien we het andere horizontaal weg. Welke van de twee voorwerpen zal het eerste op de grond komen ?
Wat we waarnemen is een voorbeeld van het
onafhankelijkheidsprincipe. De horizontale
beweging heeft geen invloed op de verticale beweging. Beide voorwerpen komen tegelijkertijd op de
grond.
In formele bewoording luidt het
onafhankelijkheidsprincipe :
Wanneer een voorwerp tegelijkertijd onderworpen is aan twee bewegingen, dan is zijn positie na een bepaald tijdsverloop dezelfde als wanneer die twee bewegingen, telkens gedurende hetzelfde tijdsverloop, na elkaar en onafhankelijk van elkaar gebeuren.
Of anders geformuleerd :
Twee of meer bewegingen die tegelijkertijd plaatsgrijpen, blijven hun volledige uitwerking behouden.
3.2 De horizontale worp
3.2.1 Beschrijving van de beweging
Een eerste toepassing die we bekijken is de horizontale worp. Bij een horizontale worp lanceren we een voorwerp horizontaal met een beginsnelheid v0 vanop een hoogte y0. Eens gelanceerd, zal het voorwerp onder invloed van de zwaartekracht naar beneden bewegen, terwijl het door zijn horizontale snelheid eveneens verder zal bewegen.
De horizontale worp is de samenstelling van een valbeweging en een eenparig rechtlijnige beweging.
Om de beweging te beschrijven kiezen we X-as evenwijdig met de grond, en de Y-as zo dat deze door de beginpositie loopt. Dit geeft als beginsituatie :
Afbeelding 24:
Stroboscopische opname van een voorwerp in vrije van en een voorwerp dat tegelijkertijd horizontaal wordt weggeschoten. (Bron : Physics -Serway)
Afbeelding 25: De horizontale worp is een samenstelling van een eenparig rechtlijnige beweging en een valbeweging.
x t
0=0
y t
0=
y
0De horizontale worp is een samenstelling van een eenparig rechtlijnige beweging in horizontale richting en een valbeweging in verticale richting. Dit geeft als
positievergelijkingen :
x t=v
0⋅
t
y t= y
0−
1
2
g t
2Door t te elimineren krijgen we de vergelijking van de baan in het x,y-vlak :
t=
x
v
0y= y
0−
1
2
g
x
2v
02Dit is de vergelijking van een parabool. De baan die het voorwerp zal beschrijven zal dus parabolisch zijn.
3.2.2 Berekenen van de dracht
De afstand die het voorwerp in horizontale richting zal afleggen vooraleer de grond te raken (ook wel dracht genoemd), kunnen we eveneens bepalen uit de bewegingsvergelijkingen.
Allereerst berekenen we de tijd t1 nodig om vanop beginhoogte tot op de
grond te komen. Dan bekijken we welke afstand gedurende die tijd is afgelegd in horizontale richting, en we hebben de dracht !
Op t1 raakt het voorwerp de grond. Dan is bijgevolg :
y t
1=0 m
y
0−
1
2
g t
1 2=0 m
t
1=
2 y
0g
x t
1=
v
0t
1x t
1=
v
0
2 y
0g
3.3 De projectielbeweging (schuine worp)
3.3.1 Beschrijving van de beweging
Onder een schuine worp verstaan we een voorwerp dat gelanceerd wordt met een beginsnelheid v0, onder een zekere hoek α met de horizontale, vanop een hoogte y0. Om de berekeningen enigszins te vereenvoudigen,
veronderstellen we dat we vertrekken vanop de begane grond, en dat bijgevolg
y0 = 0m.
We kunnen de initiële snelheidsvector ontbinden in een horizontale en een verticale component :
v
0=
v
0, x
v
0, y waarbijv
0, x=
v
0cos
v
0, y=
v
0sin
Eens het projectiel gelanceerd, is het in verticale richting onderhevig aan de valversnelling. (aan
welke versnelling is het onderhevig in horizontale richting ?). We kunnen de projectielbeweging
bijgevolg beschouwen als een samenstelling van een eenparig rechtlijnige beweging in de horizontale richting en een verticale worp.
Afbeelding 28: De schuine worp is een samenstelling van een ERB en een verticale worp.
Afbeelding 27: ontbinding van de initiële snelheidsvector in componenten.
3.3.2 De bewegingsvergelijkingen
De projectielbeweging kan ontbonden worden in een ERB in horizontale richting en een verticale worp.
De snelheidsvergelijkingen worden dus :
v
x
t=v
0, xv
y
t =v
0, y−
g t
En de positievergelijkingen :x t=v
0, xt
y t=v
0, yt−
1
2
g t
2Wat worden deze vergelijkingen als we vertrekken van op een beginhoogte y0 in
plaats de begane grond ?
Als we uit bovenstaande vergelijkingen t elimineren, verkrijgen we de
vergelijking van de baan :
t=
x
v
0, xy=
v
0, yv
0, xx−
1
2
g
v
0, x2x
2Dit is de vergelijking van een parabool. De baan die het voorwerp zal beschrijven zal dus parabolisch zijn.
Afbeelding 29: Evolutie van de snelheidsvector bij een schuine worp. Kan je ook overal de versnellingsvector bijtekenen ?
3.3.3 Berekenen van de dracht
Gebruik makend van het onafhankelijkheidsprincipe, berekenen we eerst de
tijd nodig om terug op de grond te raken, en met dat resultaat berekenen
we de afstand die in die tijd in horizontale richting is afgelegd. We noemen t1 het tijdstip waarop het projectiel de grond raakt. Dan is :
y t
1=0
v
0, yt
1−
1
2
g t
1 2=0 m
t
1
v
0, y−
1
2
g t
1=0 m
Hieruit volgt dat ofwel
t
1=0 s
ofwel
t
1=2
v
0, yg
Het laatste resultaat is van belang voor het berekenen van de dracht. (Wat
betekent het eerste resultaat ?)
De dracht bepalen we dan :
x t
1=2
v
0, xv
0, yg
x t
1=2
v
0 2sin cos
g
x t
1=
v
0 2sin 2
g
Voor welke hoek is de dracht maximaal ?
Oefening : toon aan dat de maximaal bereikte hoogte gegeven wordt door
y
max=
1
2
v
02sin
2
g
3.4 Oefeningen
3.4.1 Voorbeelden
a Voorbeeld 1 Opgave :Een kogel wordt in horizontale richting met een snelheid van 800 m/s afgeschoten op een schietschijf die zich op 100 m afstand bevindt. Als de schutter precies op de roos mikt, over welke afstand is de kogel afgezakt als hij de schijf treft ?
Gegevens :
v
0=800
m
s
x t
0=0 m
y t
0=
0 m
x t
1=100 m
Gevraagd :y t
1=
?
Oplossing :Het gaat hier duidelijk over een horizontale worp. Gebruik makend van de bewegingsvergelijkingen berekenen we eerst t1, waaruit y(t1) zal volgen.
x t
1=
v
0t
1t
1=
x t
1
v
0Met dit resultaat :
y t
1=−
1
2
g t
1 2y t
1=−
1
2
g
x t
1
2v
02Invullen van gegevens levert :
y t
1=−
1
2
9,81
m
s
2100 m
2800
m
s
2y t
1=7,66⋅10
−2m
Antwoord :De kogel zal 7,66 cm gezakt zijn.
b Voorbeeld 2
Opgave
Een projectiel wordt met een beginsnelheid van 350 m/s onder een hoek van 30° met de horizontale afgeschoten. Hoelang duurt het tot het projectiel terug de grond raakt en welke afstand heeft het dan overbrugd ?
v
0=350
m
s
x t
0=0 m
y t
0=
0 m
=30 °
y t
1=0 m
Gevraagd :t
1=
?
x t
1=
?
Oplossing :Het tijdstip waarop het projectiel de grond raakt halen we uit de bewegingsvergelijkingen :
y t
1=0
v
0, yt
1−
1
2
g t
1 2=0 m
t
1
v
0, y−
1
2
g t
1=0 m
Hieruit volgtt
1=2
v
0, yg
=
2 v
0sin
g
Gegevens invullen levert :
t
1=
2⋅350
m
s
⋅
sin 30 °
9,81
m
s
2t
1=3,56⋅10
1s
Hiermee bepalen we dan de overbrugde afstand :
x t
1=
v
0cos ⋅t
1x t
1=350
m
s
cos30 °⋅3,56⋅10
1s
x t
1=1,08⋅10
4m
Antwoord :3.4.2 Opgaven
1. Iemand tracht loodrecht een 300 m brede rivier over te zwemmen met een snelheid van 1,00 m/s. Als de stroomsnelheid 1,50 m/s is, in welke tijd bereikt hij dan de overzijde en hoe ver zal hij afgedreven zijn ? Construeer de snelheidsvector en bereken de grootte van de resulterende snelheid.
2. Een stuntman rijdt met zijn auto over een horizontale weg naar een kloof toe. De kloof is 10 m breed, en de overkant ligt 3 m lager. Welke snelheid moet de wagen ten minste bezitten opdat de stunt zou slagen ?
3. Vanop een toren wordt een steen horizontaal weggegooid met een snelheid van 10 m/s. Hij komt op de grond terecht, 50 m van de toren verwijderd. Bereken de hoogte van de toren (luchtweerstand verwaarlozen).
4. Een auto gaat aan het slippen op een weg met een snelheidsbeperking van 50 km/h en rijdt door een brugleuning boven een rivier. Hij komt 5,2 m lager in het water terecht en blijft gedeeltelijk boven water uitsteken. De politie doet opmetingen en stelt vast dat de auto 22 m ver van de brug terecht gekomen is. Hoe groot was zijn snelheid ten minste ? Was die in werkelijkheid groter of kleiner ?
5. Vanaf een rots aan de rand van een meer, schiet men een kogel horizontaal af. De rots bevindt zich op 19,6 m boven het wateroppervlak. De kogel komt 2500 m verder in het water terecht. Bereken de snelheid waarmee de kogel is afgevuurd.
6. Uit een tuinsproeier die gericht is onder een hoek van 60° met de horizontale stroomt het water met een beginsnelheid van 25 m/s. Bereken hoe ver de sproeier reikt.
7. Een speerwerper gooit de speer weg van op schouderhoogte (1,80 m) met een beginsnelheid van 12 m/s onder een hoek van 45°. Wat is de maximaal bereikte hoogte en hoe ver komt de speer terecht ?
8. Een oorlogsbodem heeft een vijandelijk schip ontdekt aan de andere kant van een eiland, dat pal tussen hen ligt. De afstand tussen de twee boten bedraagt 15 km. De hoogste heuveltop op het eiland ligt 1120 m boven zeeniveau, en ligt juist op de verbindingslijn tussen beide schepen. Onder welke hoek moet de kanonnier zijn kanonnen richten om het vijandelijk schip te raken, als hij weet dat de snelheid van de granaten bij het verlaten van de loop 550 m/s bedraagt ?
4 De wetten van Newton
Om de notaties enigszins te vereenvoudigen spreken we af dat we de grootte van een vector noteren met hetzelfde symbool als de vector, maar zonder pijltje erboven. Zo is
●
F
de krachtvector, en●
F
de grootte van die krachtvector.4.1 Eerste wet van Newton
4.1.1 Traagheidsbeginsel
Dit beginsel ken je nog uit de cursus van het 4e jaar. We herhalen het kort :
Een object in rust blijft uit zichzelf rust.
Eenmaal in beweging, zal een object uit zichzelf deze beweging eenparig rechtlijnig verder zetten.
4.1.2 Het concept kracht
Volgens het traagheidsbeginsel kan een voorwerp zijn bewegingstoestand
niet zelf wijzigen. Om vanuit rust in beweging te komen, om te versnellen of
te vertragen, of om tot stilstand te komen, moet er bijgevolg een externe
oorzaak zijn.
Een dergelijke externe oorzaak noemen we een kracht.
Is het zo dat op een voorwerp dat eenparig rechtlijnig beweegt of in rust is, geen krachten inwerken ? Nee, verre van, op een voorwerp in rust kunnen meerdere krachten werkzaam zijn, maar ze zullen elkaars effecten opheffen.
We kunnen het traagheidsbeginsel dan ook herformuleren als :
Een voorwerp is in rust of beweegt volgens een eenparig rechtlijnige beweging, als en slechts als de resultante van de inwerkende krachten de nulvector is.
F
R=
∑
F
i=
0
Afbeelding 30: Een vliegtuig kan slechts éénparig rechtlijnig vliegen, als de som van alle inwerkende krachten (welke zijn dat ?) de nulvactor is. (bron : www.nasa.org)
4.1.3 Bepalen van de resulterende kracht
Krachten zijn vectoren, je kan niet zomaar de groottes optellen om dan tot de resulterende kracht te komen.
F
1
F
2 is niet hetzelfde alsF
1
F
2 ! Wat is het verschil ?Je hebt vorig jaar al een aantal technieken gezien om de resulterende kracht
F
R=
F
1
F
2 van twee inwerkende krachtenF
1 enF
2 te bepalen:● Als
F
1 enF
2 dezelfde richting en zin hebben, dan heeft
F
R=
F
1
F
2 eveneens dezelfde richting en zin, en isF
R=
F
1
F
2 .● Als
F
1 enF
2 dezelfde richting maar tegengestelde zin hebben, dan heeftF
R=
F
1
F
2 eveneens dezelfde richting, de zin van degrootste kracht en is
F
R=∣
F
1−
F
2∣
.● Als
F
1 enF
2 verschillende richtingen hebben, kon je deparallellogramregel toepassen, en op grafische wijze de resultante
bepalen.
Het grafisch bepalen van de resulterende kracht zou nogal omslachtig kunnen worden als we bvb. de resultante van twee krachten met groottes van resp. 53 N en 76 N willen bepalen, die een hoek insluiten van 23°.
Afbeelding 31: Samenstellen van krachten met zelfde zin en richting.
Afbeelding 32: Samenstellen van krachten met zelfde richting, maar tegengestelde zin.
Afbeelding 33: Samenstellen van krachten met verschillende zin en richting.
Veronderstel dat we twee krachten
F
1 enF
2 hebben met verschillende richting en zin, en dat we de resultanteF
R=
F
1
F
2 moeten berekenen.Ontbinden we beide krachten in componenten volgens X- en Y-as :
F
1=
F
1, x
F
1, y
F
2=
F
2, x
F
2, y Zij α de hoekF
1 van met de X-as, en β de hoek van
F
2 met de X-as, dan zijn :F
1,x=
F
1cos
F
1, y=
F
1sin
enF
2, x=
F
2cos
F
2, y=
F
2sin
Nu is
F
R=
F
1
F
2
F
R=
F
1, x
F
1, y
F
2, x
F
2, y
F
R=
F
R , x
F
R , yAfbeelding 34: We moeten de resultante berekenen van twee krachten die een willekeurige hoek insluiten.
Afbeelding 35: Ontbinding van de eerste kracht in componenten volgens X en Y as.
Afbeelding 36: Ontbinding van de tweede kracht in componenten volgens X en Y as.