Natuur, leven en technologie

Staatsexamen VWO

2017

Natuur, leven en technologie

Tijdvak 1 Vrijdag 19 mei 09.00 – 11.00 uur

College-examen schriftelijk

Opgavenboekje

Voor dit examen zijn maximaal 57 punten te behalen; het examen bestaat uit 26 vragen: 23 open en 3 gesloten vragen.

Het examen duurt twee uur.

Voor elke vraag is aangegeven hoeveel punten met een goed antwoord behaald kunnen worden.

Bij de beantwoording van enkele vragen moet het BINAS tabellenboek 6e druk geraadpleegd worden.

Het gebruik van een grafische rekenmachine is toegestaan.

Als bij een open vraag een verklaring, uitleg of berekening wordt gevraagd, worden aan het antwoord meestal geen punten toegekend als deze verklaring, uitleg of berekening ontbreekt.

Geef niet meer antwoorden (redenen, voorbeelden e.d.) dan er worden gevraagd.

Als er bijvoorbeeld twee redenen worden gevraagd en je geeft meer dan twee redenen, dan worden alleen de eerste twee in de beoordeling meegeteld.

Geef het antwoord van meerkeuzevragen in duidelijke hoofdletters.

- Tenzij anders vermeld, is er sprake van normale situaties.

Mercurius

Mercurius is de dichtst bij de zon staande en tevens kleinste planeet in ons zonnestelsel. De planeet is vernoemd naar de Romeinse god Mercurius, de boodschapper van Jupiter (zie figuur 1), vanwege de snelle draai om de zon alsof hij een boodschap moet doen. Net als de Aarde is het een terrestrische planeet met een vast oppervlak dat veel

overeenkomsten vertoont met dat van de Maan. Opmerkelijk is dat deze kleine planeet een vrij sterk magnetisch veld vertoont. Mercurius heeft

geen manen.

3p 1 - Bereken de omlooptijd van Mercurius in dagen, met

behulp van de nauwkeurige cirkelbaanwet van Kepler.

Die luidt in formule:

3 2 1 2 2

)

(

4

r

m

m

G

T

⋅

+

=

π

Bedenk hierbij welke waarden u voor r en m moet invullen.

- Vergelijk de berekende omlooptijd met de

omlooptijd zoals vermeld in Binas. Verklaar eventueel het verschil.

- Speelt de massa van Mercurius een belangrijke rol in de berekening?

Leg je antwoord uit.

3p 2 - Leid de formule voor de ontsnappingssnelheid af uit

de formule voor de gravitatie-energie in het oneindige.

- Bereken daarmee de massa van een zwart gat waarvan de Schwarzschildstraal even groot is als Mercurius.

Excentriciteit is de verhouding tussen de lange en korte as van een baan en geeft weer hoe ellipsvormig

deze baan is. Figuur 1: Mercurius

Hierin is e de excentriciteit, a de lange as van de ellips en b de korte as. Mercurius heeft een excentriciteit van 0,0554

Een regenmeter

Bekijk het model van een regenmeter (figuur 2) in figuur 3.

Figuur 2: Een regenmeter

Figuur 3: Model van een regenmeter

Een regenmeter is een bak die gebruikt wordt om de regenval (in mm/uur) te meten. De

regenmeter heeft aan de bovenzijde een oppervlakte (in m2), die bepaalt hoeveel water het

op kan vangen. Een onderdeel van het model is een "lek" dat zorgt voor het weglekken van water door een gaatje. Het gaatje doet aan het begin nog niets (want de grootte van dit gaatje is dan nul). De hoeveelheid water in de regenmeter is gegeven in de eenheid liter.

1p 4 Hoe noemt men in een grafisch modelleerprogramma een symbool dat onafhankelijk is van

andere symbolen en dat alleen van buitenaf kan worden veranderd?

A Een constante B Een variabele

C Een voorraadgrootheid

2p 5 Waar hangt de instroom van de regenmeter vanaf?

A Alleen van de oppervlakte. B Alleen van de regenval.

C Van de oppervlakte en de regenval.

D Van de oppervlakte, de regenval en de waarde van "regenmeter".

2p 6 Bereken hoeveel liter water de regenmeter in 24 uur opvangt, als het continu regent met

een snelheid van 10 mm/uur.

Nu maken we een gaatje onder in de regenmeter. Hierdoor werkt hij niet goed meer. Hoe groter het gat, hoe slechter hij werkt: het water lekt weg.

2p 7 Waar hangt de lekhoeveelheid van de regenmeter nu direct vanaf?

A Van de straal van het gaatje en de regenval. B Van de waterhoogte.

C Van de waterhoogte en de regenval.

D Van de waterhoogte en de straal van het gaatje.

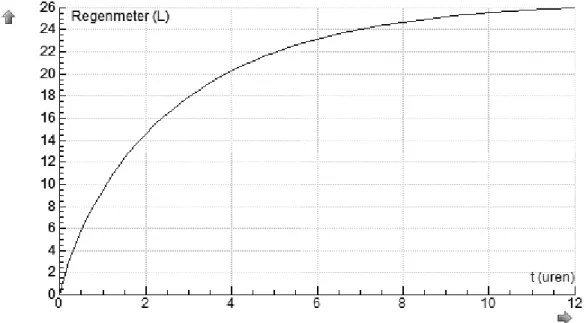
Bekijk figuur 4, die laat zien wat er gebeurt als je het model van de regenmeter laat rekenen met een gat met een diameter van 1,4 dm.

Figuur 4: De vulling van een regenmeter met een gat met een diameter van 1,4 dm

1p 8 Verklaar de vorm van deze grafiek.

Onderzoek aan de hersenen

Iemand die alles wil weten over neuronen heeft kennis nodig uit biologie, natuurkunde en scheikunde. Vaak gebruiken wetenschappers uit verschillende vakken voor dezelfde of zeer verwante begrippen dezelfde termen, maar soms ook verschillende.

Vergelijk onderstaande begrippen uit de biologie en de natuurkunde. - Een membraan van een neuron dat wordt geprikkeld;

- Een koperdraad die aangesloten is op het stopcontact. Bij beide is er sprake van verplaatsing van lading.

3p 9 Neem onderstaande tabel over op je antwoordblad en vul deze in.

Membraan Koperdraad

Ladingdragers

Naam van grootheid met eenheid Volt

Levering van energie voor transport door

2p 10 Beschrijf hoe je de elektrische activiteit in een zenuwcel kunt meten.

Noem het meetinstrument en geef aan wat je moet doen om de meting uit te voeren.

De snelheid waarmee een impuls wordt doorgegeven ligt bij de mens tussen 70 en 120 m/s. Neem aan dat de snelheid bij een bepaald neuron 80 m/s is.

2p 11 Bereken de tijd in microseconden die nodig is om een impuls een afstand van 0,12 cm af te

laten leggen.

De spanning door een koperdraad wordt met 2/3 van de lichtsnelheid doorgegeven.

2p 12 Bereken hoeveel keer sneller een signaal door koperdraad gaat ten opzichte van de

snelheid van dat bepaalde neuron.

1p 13 Op welke manier is er in het lichaam van bijvoorbeeld de mens gezorgd door een speciale

constructie van de neuronen dat de impulsgeleidingssnelheid veel hoger is dan bij dieren zonder die constructie, zoals bijvoorbeeld slakken? Gebruik eventueel Binas.

Een scheikundige is vooral geïnteresseerd in de moleculaire processen in de neuronen.

2p 14 Noem de vier elementen waarvan de ionen een belangrijke rol spelen bij die processen.

Levensduur van de Zon

Figuur 5: De levenscyclus van de zon

Om via een berekening te schatten hoe lang de Zon nog meegaat, moet men eerst een paar zaken weten.

In de Zon vindt als onderdeel van de proton-protoncyclus het volgende proces plaats:

ν

+

+

→

+

e

H

H

H

De gehele proton-protoncyclus vertoont een massadefect van 0,029 u. Bij één zo’n cyclus komt volgens tabel 7 in Binas dus 0,029 u × 931,49 MeV / u = 27,0132 MeV energie vrij. Dit

is gelijk aan 4,33·10−12 J. Om te berekenen hoe lang de Zon nog mee zal gaan, kun je

onder andere het volgende gegeven gebruiken: de zon straalt per seconde 3,90·1026 J aan

energie uit.

Jan zegt: “Nu kun je als volgt berekenen hoe lang de Zon nog meegaat: 3,90·1026 : 4,33·10−12 = 9,011·1037 s.

Hanneke zegt: “Dat kan niet goed zijn. De zon wordt volgens wetenschappers nooit zo oud.”

2p 16 Laat aan de hand van dit aantal seconden en figuur 5 zien dat Hanneke gelijk heeft.

Hanneke zegt dat de eenheid s in de uitkomst van Jan niet klopt en dat hij uitgerekend heeft hoeveel neutrino’s er per seconde op de zon ontstaan.

1p 17 Laat aan de hand van een eenhedenberekening zien dat Hanneke ook nu gelijk heeft.

Het aantal neutrino’s dat er per seconde op de zon ontstaan (dus hoeveel proton-protoncycli per seconde) is bekend.

Ga ervan uit dat de zon nog voor 70 massa% uit waterstof bestaat, dan is uit te rekenen hoe lang de zon er over zal doen heel haar huidige massa (zie Binas 32C) aan waterstof te fuseren tot helium, waarvoor per proton-protoncyclus telkens vier protonen nodig zijn. Neem aan dat dit het enige proces is op de Zon.

3p 18 Bereken hoe lang de Zon op basis van deze aannamen nog zou kunnen meegaan in

miljarden jaren.

Kogels in het water

In veel actiefilms duikt de held in het water om te ontkomen aan een regen van kogels. Hij zwemt een stuk onder water en komt daarna ongedeerd weer boven. Is dit realistisch? En op welke diepte moet de actieheld dan zwemmen?

Water geeft een grotere weerstand dan lucht. De luchtweerstand is de wrijvingskracht die de lucht uitoefent op een voorwerp, als dit zich door de lucht voortbeweegt. Op analoge wijze wordt weerstand ondervonden van elk ander medium waarin een voorwerp zich voortbeweegt. De formule voor luchtweerstand geldt niet alleen voor lucht, maar ook voor andere gassen en vloeistoffen.

Formule voor de luchtweerstand:

Daarin geldt:

F = de wrijvingskracht die op het voorwerp werkt tijdens de beweging in Newton

ρ = de dichtheid van de stof waarin het voorwerp zich voortbeweegt in kg·m-3

ν = de snelheid in m·s-1

A = frontaal oppervlak van het voorwerp in m2

Cw = vormcoëfficiënt

2p 19 Leid uit de formule af wat de eventuele eenheid van de vormcoëfficiënt is. Gebruik hierbij

Binas tabel 4.

3p 20 Laat met een berekening zien dat de afstand die een kogel in water aflegt ongeveer 1,8 m

is als de zwaartekracht buiten beschouwing wordt gelaten. Bereken die afstand met behulp van formules uit Binas tabel 35A4 en de bovenstaande formule voor de luchtweerstand. Bij

het afremmen van de kogel in het water mag je ervan uitgaan dat de gemiddelde kracht 40% van de maximale remkracht bedraagt.

Maak hierbij ook gebruik van de volgende gegevens: Massa kogel = 2,592 gram

Diameter kogel = 2,15 mm Vormcoëfficiënt = 0,295

Snelheid raken water = 300 m/s

In het programma Checkpoint van NPO Zapp werd door presentatrice Rachel Rosier (zie figuur 6) met een experiment onderzocht door hoeveel water een kogel wordt

tegengehouden. Bij dit experiment legden zij tien waterballonnen, met een doorsnee van ongeveer 30 cm, op een rij. Vervolgens werd er op deze ballonnen geschoten. De kogel bleek door drie waterballonnen te gaan, de overige ballonen bleven heel. Dit komt niet overeen met de theoretische waarde uit opgave 20.

Figuur 6: Rachel Rosier van Checkpoint

2p 21 Noem twee variabelen in de proefopstelling die verantwoordelijk kunnen zijn voor dit

verschil.

3p 22 Beschrijf een mogelijke proefopstelling van een experiment waarmee je wel hetzelfde

resultaat als in opgave 20 kunt verwachten.

Katchalsky-machine

Met behulp van de Katchalsky-machine kan ‘blue energy’ worden opgewekt. De techniek is

bedacht door de Israëlische biofysicus Katchalsky (1914-1972). Hij constateerde dat de stof collageen in zout water krimpt en in zoet water weer rekt.

Collageen is opgebouwd uit met elkaar verbonden microfibrillen, die op hun beurt bestaan uit drie met elkaar verstrengelde polypeptideketens (zie figuur 7). Deze polypeptideketens

zijn de meest fundamentele bouwstenen van het collageen en bestaan uit herhalingen van een aminozuurmotief: glycine-X-Y. Hierbij is het aminozuur op de X-positie meestal proline en op de Y-positie meestal hydroxyproline. Hydroxyproline ontstaat door substitutie van een

OH-groep aan de middelste CH2-groep van proline. Hydroxyproline en proline spelen een

sleutelrol in de stabiliteit van collageen. Ze maken de scherpe draaiing van de

collageenhelix mogelijk. De aanwezigheid van een OH-groep vergroot de stabiliteit van het collageen.

Figuur 7: Opbouw van collageen

De aanwezigheid van glycine, dat geen aminozuurresidu bezit, zorgt ervoor dat de drie polypeptideketens elkaar voldoende kunnen naderen en met elkaar intermoleculaire interacties, voornamelijk waterstofbruggen, kunnen aangaan. Collageenmoleculen nemen gemakkelijk watermoleculen op. Hierdoor wordt onder andere de ruimte tussen de

microfibrillen groter. Het krimpen in zout water wordt veroorzaakt door osmotische werking.

4p 23 Teken de structuurformule van de repeterende eenheid in collageen.

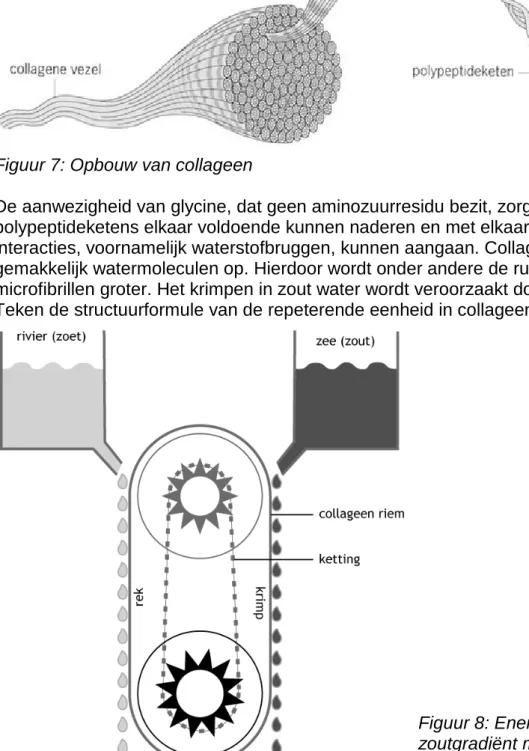
Figuur 8: Energiewinning uit een zoutgradiënt met de Katchalsky-machine

In de Katchalsky-machine (zie figuur 8) draait een riem van collageen over twee schijven. De schijven zijn met een ketting verbonden via tandwielen met een verschillende straal. Als de collageenriem in contact komt met zout water, krimpt de riem en komt er druk op de riem te staan. Doordat de collageenriem over de onderling verbonden schijven loopt, kan de riem maar één kant op draaien om de druk te verdelen. Voor de twee tandwielen geldt

onderstaande formule:

F

· r

= F

· r

F1 is de kracht op het ene wiel, r1 de straal van dat wiel. F2 is de kracht die op het andere

tandwiel werkt, en r2 is de straal van dat tandwiel.

2p 24 Leg met behulp van de tekst uit waardoor de collageenriem krimpt als de riem in aanraking

komt met zout water.

2p 25 Beredeneer welke kant de ketting in de Katchalsky-machine in figuur 8 opdraait.

Als het gekrompen collageen door de beweging in de zoetwaterstroom terecht komt, wordt het zoute water weer weggespoeld, waardoor de collageenriem weer naar zijn normale

grootte uitzet. Hierna zal het proces zich herhalen.Als op een van de wielen een generator

wordt aangesloten, kan uit deze beweging elektrische stroom gehaald worden.

2p 26 Noem een voor- en een nadeel van de Katchalsky-machine ten opzichte van de Reverse